Impact Factor : 0.548
- NLM ID: 101723284
- OCoLC: 999826537
- LCCN: 2017202541
Hyun Soo Lim1* and Necla Kenar2
Received: August 25, 2017; Published: September 13, 2017
Corresponding author: Hyun Soo Lim, Department of Electrical and Electronics Engineering, Faculty of Technology, T-4 Building, Sakarya University, Esentepe Campus, 54050 Serdivan-Sakarya, Turkey
DOI: 10.26717/BJSTR.2017.01.000357
This paper proposes a method of accurate light distribution using the Monte Carlo Simulation. In a Photodynamic Therapy (PDT), accurate light penetration depths are especially important as it is to be expected that applying too little light or too much light could result in inadequate tumor cell kill. The basic theory of this method is statistical iteration of simulation at phantom medium and can model any complex condition in biological tissues without any kind of tool. We performed Monte Carlo simulation with phantom layer having the optical properties of biological tissues. In this result, we could obtained the acceptable light dosimetry in biological phantom. Monte Carlo simulation is very powerful approaching model in radiation transfer for solving a variety of physical and mathematical problems.
Keywords: Monte Carlo Simulation; Light Distribution; Photodynamic Therapy (Pdt); Optical Properties
Recently, Photodynamic therapy (PDT) method becomes one of the methods to treat cancer using light. It is necessary to measure the light dosimetry in tissue to apply PDT for cancer to patient. To measure light dosimetry accurately, One must understand the light propagation in tissue and simulate with optical properties of target tissue. Optical coefficients are basically three interaction coefficients: absorption coefficient (μa), scattering coefficient (μs) and phase function [1-4]. It is very important to measure the correct optical properties in biological tissue to execute Monte Carlo simulation. If one want to perform with correct optical properties in simulation, he should have to measure the light doses in biological tissue. In this study, we simulated Monte Carlo simulation with multi-layered phantoms, having the optical properties in biological tissue, to evaluate the light fluence profile.
Basically, photons with wavelength of 600 to 1000nm, the light of phototherapeutic window, have the maximum penetration power because of the component of tissue have lower absorption coefficient in this region. If the incident light intensity is 1/e and the wavelength of the incident light is 700 nm, the penetration depth is 2 cm in white skin or 1.5 cm in black skin. The light scattering in biological tissue depends on Henyey-Greenstein phase function. Jacques et al. (1987) have experimentally evaluated that the Henyey-Greenstein phase function is well represent the single scattering in tissue [5]. The phase function is
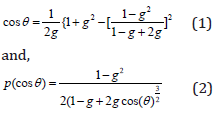
The value of g, the anisotropic factor, in tissue is between 0.3 and 0.98, but g is about 0.9 in visible light region.
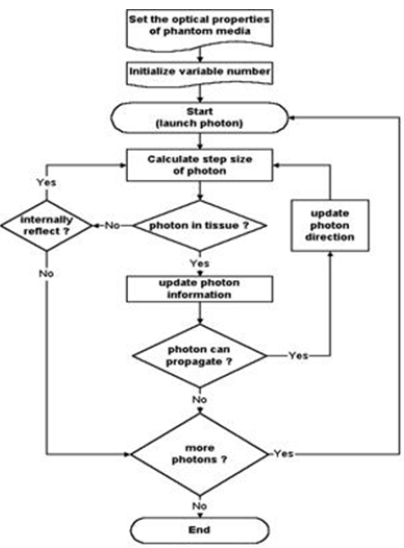
The flowchart of Monte Carlo simulation is shown (Figure 1) [4]. The first step is that one must decide the phantom media to simulate and the optical properties of phantom media. And then, initialize all variables in program. The informations of photon to initialize are the intensity of photon, the number of photon to simulate, and the incident direction. Next, run Monte Carlo program. One must initialize the photon information whenever each photon is launched. The moving step (△ size s) of photon in biological tissue is determined by random number ξ and the attenuation coefficient of tissue using Eq.3.
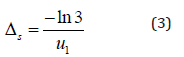
Figure 3: Flowchart of Monte Carlo Simulation.
The intensity of photon is decreased by some amount when photon is moved. If the intensity of photon is too low, one must launch new photon or terminate program to evaluate the results. The detail informations of photon are updated when photon is moved. The light scattering and the angular dependence of photon is determined by Henyey-Greenstein phase function. The penetration depth of photon is determined by the attenuation coefficient of biological tissue and the intensity of photon. The probability of internal reflection of photon is determined by Fresnel reflectance coefficient R(θi) [3].
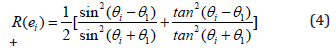
In this study, Monte Carlo simulation is performed with matched boundary condition. The refract index of each phantom layer is 1.37. The refractive index of ambient material is 1.
To run Monte Carlo simulation, we used standard C/C++ in PC (Windows). One can run this program other computer (Macintosh, Workstation, etc). We performed Monte Carlo simulation in imaginary layer such as Table 1. Each optical property in Table 1 is the value of human tissue measured at 630nm in vitro. First, we evaluated the Monte Carlo simulation in two situations for 106 photons. In the first situation, absorption coefficient and scattering coefficient are variable, but g is not.
Second situation is that g is variable, but absorption coefficient and scattering coefficient is not. The results of second situation are shown in Figure 2. As shown in Figures 2 & 3, we found that light propagation characteristics in biological tissue depend on the optical properties of their tissue. In these result, we can obtain the maximum penetration depth of each layer having different optical properties. We obtained Figure 4 by simulating the multi-layered phantom media with parameters given in Table 1.
Figure 5: The result of first situation: absorption coefficient and scattering coefficient are variable, but g is not.
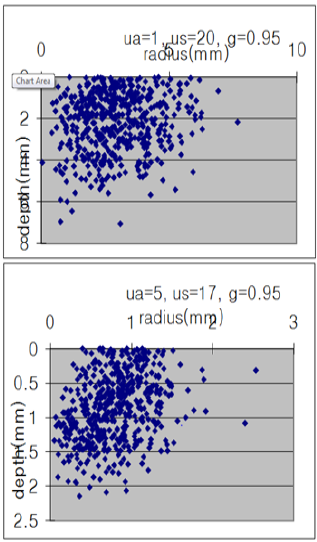
Figure 6: The result of second situation g is variable, but absorption coefficient and scattering coefficient is not.
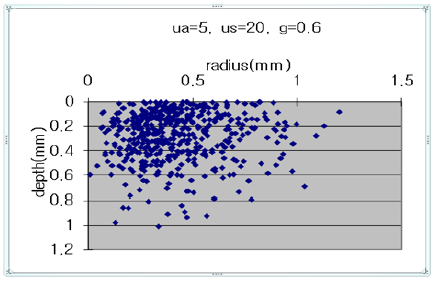
Figure 7: The result of multi-layered phantom using parameters in (Table 1).
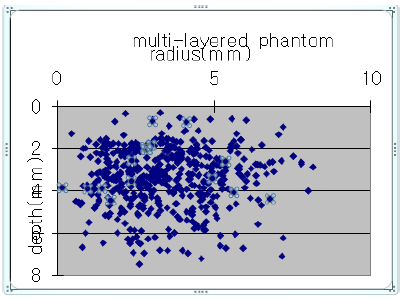
Using this light distribution profile, we can apply it PDT treatment. Of course, its data is too simple and it has a little information. But, it is appreciable that we can simulate the phantom layer in regardless of the complexity of phantom layer and the geometry of source. Also, we could compute so many physics quantity without solving transport equation. But this major disadvantage is that its simulation time is too long. It is so unnecessary. So, there is Condensed Monte Carlo simulation to reduce simulation time. Also, we suggest that it is possible to reduce simulation time tremendously with the mathematic reduction technique. In future, Monte Carlo simulation will be more applicable to calculate the light dosimetry in Photodynamic therapy.
This research is supported by TUBITAK 1005 Program (Grant number: 116F119 On going project).


