info@biomedres.us
+1 (502) 904-2126
One Westbrook Corporate Center, Suite 300, Westchester, IL 60154, USA
Site Map
ISSN: 2574 -1241
ISSN: 2574 -1241
Received: June 21, 2017; Published: July 19, 2017
Corresponding author: E Bassey, Department of Mathematics/Statistics, Cross River University of Technology, 540252, Calabar, Nigeria
DOI: 10.26717/BJSTR.2017.01.000204
The quest to actively draw the attention of research scientist to alternative approach for the eradication of the menace of HIV and its associated pathogens, informed the decision of this present work. In this paper, we concentrated in the formulation of a set of classical improved 3-Dimensional mathematical model, using ordinary differential systems for the study of bi-linear interactions of two infectious variables (HI- virus and parasitoid-pathogen) with the human immune system, in the presence of multiple control pair treatment for the management and sustainability of low level viremia. The model were presented as an optimization control problem, primed by the maximization of uninfected CD4+ T cell count concentration under a minimized systemic cost, defined by the percentage of immunotherapies administered within a finite time interval. The method of analysis explored classical numerical methods known as Pontryagin's Maximum Principle, which led to establishment of model optimization control strategy; and the existence and uniqueness of the solution of the optimal control pair were critically viewed. Numerical computations of the model, using Runge Kutter of order 4, in a Math cad environment were demonstrated with novel precision results, which not only agreed with known existing models but also showed that the higher the amount of optimal weight factor, that enhances the toxicity of drugs; the earlier, efficient, faster and less amount of chemotherapies required for the maximization of healthy CD4+ T cell count concentration. The model justified the sustainability of low level viremia under set control chemotherapies. Thus, the methodology and use of multiple treatment factors as designed by this model is widely recommended for other related infectious diseases.
Keywords: Optimal control pair; Viremia level; Immunotherapy; Sustainability; Weight factor; Maximization Systemic cost
Continue challenges posed by the lack of précised cure for the human immunodeficiency virus (HIV), leading to evolution of the acquired immunodeficiency syndrome (AIDS), is an inevitable fatal condition, which has attracted significant number of mathematical and optimal control problem models. The complexities of HIV infection progression have often deprived a better understanding of its activity in the collapse of the immune system. Furthermore, the mechanism of HIV and its multi-facets associated pathogeneses can be viewed from set point of viruses attack on CD4+ T cells and other body functioning organism, which mainstay orchestrate natural immune response to pathogenic attack [1,2]. In-view of the above constraint, most modeling now focuses on best approach to overcome all distortion to consistent suppression of the HI-virus and elimination of any associated pathogens. Thus, the study of the dynamics of HIV infection has stepped to a more importantly, multifacets infectivity and the various immunotherapies associated with its treatments. Immunotherapy administration during early stage of the disease progression is most beneficial for the raising CD4+ T cells count [3].
Understanding the impact of these immunotherapies in the dynamics of HI-virus interaction with the host immune system can better be outlined by its percentage impacts on the CD4+ T callas evaluated by the parameters associated with infection progression. The quantitative method by which we analyze this whole lot of progression is known to be through optimal control theory. Mathematical models [4-6] studied control problems of HIV infections in varying modeling approaches, using single drug treatment and similar objective functional. Optimal therapeutic control modeling for immune system response was investigated by [7]. The model used linear optimal state evaluator in a feedback therapy to minimize the effect of measurement error. Model [2], had illustrated through mathematical modeling, the effects of cytokine interleukin-2 (IL- 2) treatment on an HIV - infected patient leading to a better understanding of immune-viral dynamics necessary to produce typical disease dynamics. Also, accounting for time dependent uncertainties as its novelty, the model [8] uses stochastic optimal control theory to develop protocols for the treatment of pathogenic diseases.
Optimal control strategy for a fully determined HIV model existed as a mathematical method for the clinical testing and monitoring of HIV/AIDS diseases [9]. The model demonstrated the CD4+ T cell measurement and viral load count, using reverse transcriptase inhibitor (RTI) as single treatment. An ordinary differential system were explored in modeling the interaction of the HIV virus and the immune system of the human body, with the optimal control represented as percentage effect, which the chemotherapy has on the interaction of the CD4+T cells with the virus was examined by [5]. Explore by the model [3], were two treatment controls on a single infection (HIV), one as immune booster and the other as delay in viral progression. In our earlier model [10], we had studies the impact of sustainability of low level viremia as a preventive measure for tackling virological failure. These two later models form the framework for this present study.
In this paper, using ordinary differential equation, we propose and formulate a classical improve 3-Dimensional mathematical model, as against existing 2-Dimensional model [3], which accounts for the optimal benefits based on the maximization of the immune system and the dynamic optimal cost of pair treatment of two infectious variables - HIV virus and parasitoid-pathogen. The model which deploy optimal control theory, is aim at studying the bi-linear interaction of two infectious variables on the immune system, with pair control immunotherapies (reverse transcriptase inhibitor - RTI and protease inhibitor PI), as treatment strategies. Explore in the model, is the utilization of Pontryagin's Maximum Principle in the analysis of the derived model and then presuppose the existence and uniqueness of the model solution and results numerically illustrated using Runge Kutter of order of precision 4 in a MathCAD environment. Therefore, the study which holistically deploy optimal control techniques, is aim at investigating a set model underline by increase in healthy cells concentration, suppression and elimination of viruses at a minimal pair treatment cost, as a clinical approach in the sustainability of low level viremia.
The RTI is an active inhibitor with exclusive characteristics of boosting the adaptive immune system, thereby preventing the integration of uninfected lymphocyte cell genomes from been infected by the viral load code, as well as elimination of cells infected by parasitoid-pathogen. In a like manner, the PI is considered a passive inhibitor which prevents and suppresses cells from replication of infectious virus particles, reduces and maintain viral load below the limit of detectable clinical assay [11]. Presumably therefore, this model is the first to address concurrently, new diverse cases of dual infectious diseases (i.e. HI-virus and parasitoid- pathogen) in the presence of multiple control treatments, as against models by [3,5,9]. The entire work is organized into five sections, with the introductory devoted to section l.In section 2, we define the model material and the methods explore. Section 3 critically views the existence of the optimal control pair, the optimization control strategy as well as uniqueness of the optimality control system. Numerical computations of the model and result analysis form the pivot of section 4. Finally, we conclude the study with exclusive insighting conclusion and leading remarks in section 5.
We present in this section, model formulation and optimal control problem statement.
The present model which projects the study a two infectious variables, using two immunotherapies as pair treatment factors is formulated with the following defined physiological variables and biological parameters as inscribed in (Table 1), below: We formulate the model equation taking into account (Table 1) below, and the following assumption.
Table 1: Variables and Parameters for optimal control pair treatment of viremia.
Assumption 1: The control classes are chosen (immunotherapies) as a measurable functions specifically bounded by some definite time interval (since treatment is a function of time due to hazardous side effect) and satisfying the condition
0 ≤ ci ≤ wi(t)≤ di < 1 , i = 1,2
Therefore, with some optimal weight factors for Tu (0) = 0,V (0) = 0, P(0) = 0, the model state system is derived as:
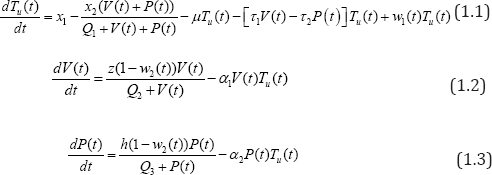
satisfying all the variables and parameters as defined in (Table 1), above.
The biological and epidemiological description of the model follows from the fact that: in equation (1.1), the term x1 -x2(V(t)+P(t))/Q1 + V(t)+P(t), define the source/proliferation of uninfected CD4+T cells, which is identify to be both external (no plasma) contribution of the cells sources such as the thymus and lymph modes and an internal (plasma) contribution from CD4+T cell differentiation; as well as external pathogen invasion. The CD4+ T cells are known to be on the degrading trend following the spontaneous infection by these viruses with limiting value xl - x2 . The value µTu(t) , represent the natural loss of uninfected CD4+ T cells, -[t1V(t)-t2P(t)Tu(t) is the gross loss by infection due to viruses.
In equation (1.2), the term z(1 - w2(t))V(t)/Q2 + V(t), accounts for the source of viral load contributions to the plasma from both external component of the lymph system and virus plasma. The choice of the lymph system is obvious as it forms the resident of viruses and become saturated in the asymptomatic stage of the disease [12]. The lymph source is with the limiting value Z . We observe a loss rate of viral load of -ɑ1V(t)Tu (t) , which includes removal of viral load due to immune response as well as viral death.
Similarly in equation (1.3),h(1 - w2(t))P(t)/Q3 + P(t) , describe the parasitoid-pathogen source of contribution to the system, with a source limiting value, h . Loss rate of parasitoid- pathogen is given as , -ɑP(t)Tu(t) which as well, incorporates elimination of parasites due to immune response and death rate of pathogen.
Since we aim at maximizing the control system, having initial values at Tu,V and P, at t0then, the objective functional is defined by
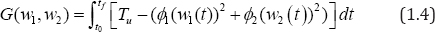
where ϕi , i=1,2 represents the optimal "weight factors" on the benefit based on the
CD4+ T cells count, which we aim at maximizing and the systemic cost, based on the percentage effects of the therapeutic treatments prong for minimization. Therefore, ϕi , i=1,2 must be positive constants which must nullify any difference in the drug severity (wi )2, i = 1,2 and thus, justified its inclusion in the quadratic functional. We queue our objective functional to characterize the optimal control pair satisfying W1* , W2*
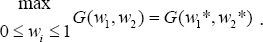
So that from equations (1.4), if wi = 1 represent maximal use of chemotherapies, then, the maximal cost is represented by . That is, (wi)2
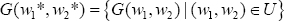
where, U = {(w1, w2)\ wimeasurable, ai ≤ wi ≤ di, t ϵ [t0, tf ], i = 1,2}, is the admissible control set.
Next we justify our model equations (1.1-1.3) by investigating the compatibility of the existence of the optimal control pair of our novel two infectious variables. We shall also, define our optimization control strategy and then, go further to prove the uniqueness of the strategy.
The existence of a two variable optimal control pair can be proved by defining the boundedness of the solutions of the system equations (1.1-1.3), for a finite time interval. This is achieve, using the fact that the super-solution 
satisfying
Are bounded on a finite time interval. We therefore resort to [12, Thm. 4.1, p. 68-69], to establish and prove the existence of the model.
Theorem 3.1. Consider the control problem with system equations (1.2-1.4). Then under assumption 1, there exists an optimal control pair
Proof: The existence of the result of the model is proved by showing that the following conditions are satisfied:
i. All the initial conditions with the controls w1 and w2 such thatwi , i=1,2 is a Lebesgue-integrable function on [t0,tf] with values in the admissible control set U , such that the state system is satisfied and not empty.
ii. The admissible control set U , is closed and convex.
iii. The right hand side (RHS) of the state system is continuous, is bounded above by a sum of the bounded control and the state, and can be written as a linear function of wi , i=1,2 with coefficients depending on assumption 1 and on the state variables.
iv. The integrand of the objective functional is concave on the admissible U , of the control set.
v. There exists consistence d1, d2 > 0 and β > 1 such that the integrand L(Tu,w1,w2) of the objective functional satisfies
Verifying these conditions, we necessarily need to invoke an existence result of [13], Thm. 9.2.1], for the existence of the state system equations (1.1-1.3), with bounded coefficients, which gives condition (i). We note that the solutions are bounded. By definition, our control set is closed and convex, and then, satisfies condition (ii). Since our state system is bilinear inw1,w2 , the RHS of (1.1)-(1.3), satisfies condition (iii), using the boundedness of the solutions. In addition, the integrand of the objective functional Tu(t) - ϕ1(w1(t))2 + ϕ2(w2(t))2 is concave on the admissible control set U . Finally, the completeness of the existence of solution of the optimal control is the fact that
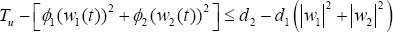
Where d2 depends on the upper bound on Tu , and d1 > 0 since ϕ1,ϕ2 > 0. Hence, we proof theorem 5.1.
Following our logical and explicit prove for the existence of an optimal control pair for a bi-variable infectious pathogen-induced HIV-1 infection priori to maximizing the objective functional (1.4), subject to control system equations (1.1-1.3), we have been able to set the basis for which we conveniently put forward the optimization control strategy of our model. Achieving this, we necessarily have to derive the conditions for the optimal control pair, using Pontryagin's Maximum Principle [14].
Theorem 3.2: Given optimal controls w1*, w2* and solutions Tu*,V*,P*, of the corresponding state system (1.2)-(1.4), there exist adjoin variables λ1,λ2, λ3 satisfying
We have proved the existence of an optimal control pair solution and as well, develop our optimization control strategy. Next, we complete the process by establishing the uniqueness of the solution for a considerable small time interval. The following theorem, strengthened by lemma 3.1(without proof) below, provides the much expected proof.
Lemma 3.1. The function w*(x)=(min(max(x,a),d)) is Lipschitz continuous in x, where a <d are some fixed positive constants.
Theorem 3.3: For t fsufficiently small, bounded solutions to the optimization system are unique.
Proof: Suppose (TuV,P,λ1,λ2,λ3) and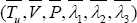 
are two different solutions of our optimization system (1.15). Let
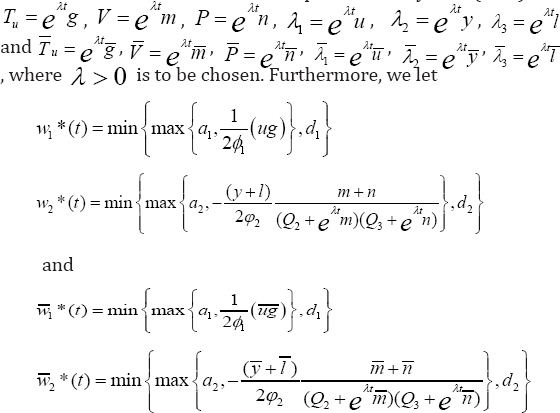
With caution, we then subtract the equations of T from 
and implementing same procedure for other state solutions. These are followed by multiplication of each of the resulting equations by appropriate difference of functions and integrate from t0 to t f . Furthermore, we proceed to sum all the six equations, from which we implore estimates to arrive at the needed unique solution. Achieving this, we invoke lemma 1, to get:
Where the constants K1 and K2 are determined by the coefficients; and the bounds on the states and adjoins. Combining these six estimates, give:
For similar proof of uniqueness of optimality system, it can be found in [3,5]. It is obvious that the uniqueness for small time interval is often in "two-point” boundary value problem resulting from opposite time orientation; the state equations containing initial conditions and the adjoin equations containing final time conditions. We see from the optimal controls that w1*, w2 * are characterized by the unique solution of the optimization control system. Thus, we obtain as above, an optimal control treatment strategy for the clinical management and sustainability of persistent low level viremia of 50 ≤ LLV < 200copies / ml [16], in an infected pathogenic-induced HIV -1 patient. The model is currently the first of it study and a typical scenario of two infectious variables under the treatment of two chemotherapies.
Furthermore, we see from the proof of theorem 3that provided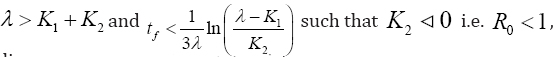 
disease-free equilibrium stateexists, which is locally asymptotically stable. Suppression and sustainability of low level viremia below detectable limits of clinical assay (see recommended guideline in [16] is strongly visible at this interval conditions. Otherwise,if 
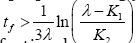such that for λ < K1 + K2,i.e. R > 1, then infection becomes endemic and is locally asymptotically unstable and globally asymptotically stable. Then, prevalence of virological failure is superimposed in the time interval.
We present some numerical computations for our optimal control system, solvable using Runge-Kutter fourth order scheme of accuracy 4, in a MathCAD environment. For a more realistic illustration, we take , see details on [17].
Computation of the model involves systematic simulation of equation (1.15), which constitute the dynamic optimal control system. Using two different treatment optimal control weight factors, φ1 = 4 and φ2 = 10, balanced by benefit functions w1= 0.4 and w2 = 0.02, having upper bounds of α2 = 20 = d2 , we compute numerically (with parameters values as in table 1), the pair treatment schedules for the optimal control of uninfected CD4+ T cell count concentration, viral load and parasitoid-pathogen progressions, as presented in (Figures 2(a-d)), without the figures of the transversality conditions for brevity. The corresponding simulation validating the benefit cost w1(t) and w2(t) as in equation (1.14), is presented in (Figure 2(d)) below. From Figure 1(a) below, we observe initial slight increase by 50mm3 for the first-three months of chemotherapy administration.CD4+ T cells then declines to near 0.07mm3 through 9 months and having apex accelerated inclination of 766.595mm3, at the 9th month interval. Decline in CD4+ T cells concentration was again observed after 10 months to 240mm3, from which stability was attained through the duration of 30 months of treatment. This signifies maximization of uninfected CD4+T cells under the above set treatment schedule. Form Figure 1 (b-c) below, infections were not eradicated but kept under control with slight gradual inclinations i.e. V (30) = 46.347mm3 and P(30) = 50.739mm3, which were still within clinical assay recommendation for suppressed and sustained low level viremia [16].
The corresponding objective functional is represented by Figure 2(d) below, indicating minimization of the systemic cost, which initially increases until after 10 months and gradually tapping to stability in the range of 0.88, after 30 months of pair chemotherapy. Further experiment explores more treatment schedule as illustrated in Figures 3(a-d) below, with Figure 3(d), corresponding to the systemic cost control. We keep the rest of the parameter values as in table 1 unchanged, with upward concentration of doses of immune boosting chemotherapy φ1 = 7.0, balance by low optimal weight factor w1(t) = 0.2.
Figure 2(a-d): Simulation of pair infection with pair treatment, w1=0.5, f 1=4, w2=0.02, f2=10.
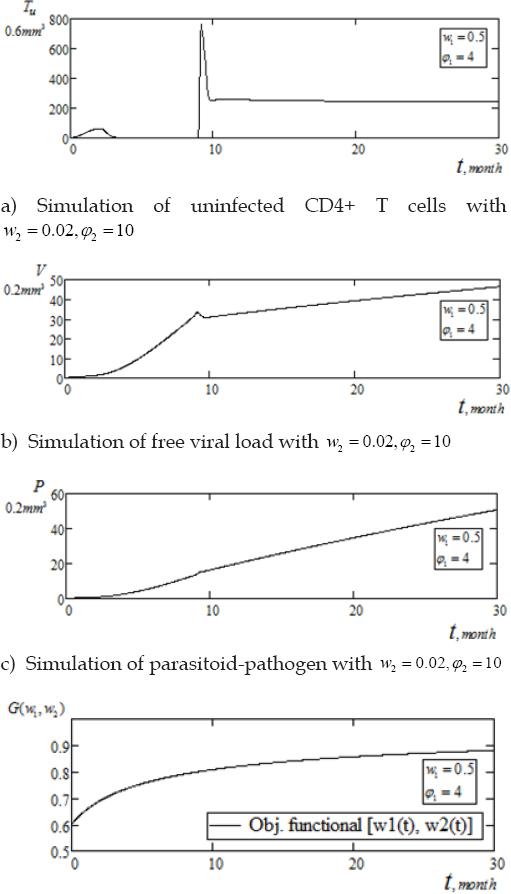
We see from Figure 3(a) below, that under the aforementioned treatment schedule, response by uninfected CD4+ T cells were characterized by similar initial behavior through the first 8 months, as in Figure 3(a). The T-cells then exhibit spontaneous increase in the range of 776.103mm3 within the same time period of 9 - 10 months. The population thereafter, fluctuated to a steady level of 300mm3 for the duration of 28 months and again inclined to 400mm3 at the tail end of 30 months. From Figures 2(b-c), viruses (HI-virus and parasitoid-pathogen), exhibits gradual linear inclination with thwarted fluctuations in the interval 9 - 10 months and thereafter showing gradual inclinations to 58.91mm3 and 75.58mm3, respectively. As shown in Figure 3(d) below, we validate the benefit cost for the second set of pair chemotherapy treatment schedule. With upward concentration of only φ = 7.0, balanced by lessened control function w1(t) = 0.2, we observe a tremendous minimization of systemic cost as benefit cost declines sharply tapping off to , after 27 months of drugs administration [17]. This outcome enhances the result of the previous treatment schedule of Figure 2(d).
Figure 3(a-d): Simulation of pair infection with pair treatment, w1=0.5, f 1=4, w2=0.02, f2=10.
The model had proposed and studied a 3-Dimensional mathematical model, which accounted for the optimality control benefits on CD4+ T cells based on the percentage effect of pair chemotherapy treatment schedule on pair infectious viruses. The method adopted here, was the presentation of the model as an optimal control problem with optimal solution established. The existence and uniqueness of model solution was critically viewed using well known technique from numerical methods - the Pontryagin's Maximum Principle and we saw that the optimization control system is defined by the state system coupled with the adjoin system with the initial and transversality conditions together with the characterization of the optimal control pair. Thus, optimality control system is a two-point boundary value problem due to state initial data and adjoin system final time data. The model was simulated numerically with combinations of model parameters.
Experimental results show that maximization of healthy CD4+ T cells concentration was higher within the asymptomatic stage of infectivity with high intensity of multiple immunotherapies as indicated by Figure 3(a). Whereas, prolong chemotherapy schedule sustains stability of healthy CD4+ T cells. Thus, leading to clinical management and sustainability of low level viremia below detectable clinical assay, provided drug regimen are sustained. Furthermore, Figure 3(d), indicates enhancement of minimization of benefit cost following a considerable prolong multiple drugs schedule.
Finally, from numerical view point, it is observable from Figures (1-2), that when immune boosting chemotherapy wi, i = 1,2 of any treatment schedule is toxic, it is systematically balanced by lessened amount of optimal weight factors φi,i = 1,2 and verse versa, leaving the more enhanced combination with the better resultant outcome. The present model in addition to been comparatively, a first study of its kind, it is in agreement with those studied by [3] with only single infection and [4-6] with only single control treatment.
In this paper, an optimization control model which accounted for two infectious variables, utilizing two immunotherapies as treatment sources were formulated. Optimization control strategy as well as numerical computations was explore in the course of investigation of best approach for maximization of free immune system concentration at affordable minimized systemic cost, taking into account definite time interval (as treatment must have definite time limit due drug resistance side-effects). Results from numerical experiments, clearly agreed to the fact that, the higher the amount of optimal weight factor, which enhances the toxicity of the drug; the earlier, efficient, faster and less amount of chemotherapies required for the maximization of healthy CD4+ T cell count concentration at minimized systemic cost under a definite small time interval. Infections were not completely eradicated but suppressed to minimum level with consistent chemotherapy schedules. The model thus, added a novel literature in HIV eradication and clinical management and sustainability of low level viremia in patients with the accompanying viruses, provided chemotherapies regimen were concurrently sustained.
My profound gratitude to my able supervisor (Prof. Lebedev, K. Andreyevich), for his positive criticisms, as this work was an integral part of my dissertation.
