Analysis of the Evaporation to Sublimation Phase Transition during Minimal Invasive Surgery Procedures via Pulsed CO₂ lasers Volume 1 - Issue 6

Franco Canestri*

• University of Tel Aviv, National Cancer Institute; Milan, Italy

Received: October 27, 2017;   Published: November 03, 2017

Corresponding author: Franco Canestri, Research Fellow (1982-1984), National Cancer Institute; Milan, Italy, Research Fellow (1993-1994, 2010), University of Tel Aviv, Tel Aviv, Israel

DOI: 10.26717/BJSTR.2017.01.000493

Abstract PDF

Objective

This Paper describes a mathematical approach to quantify the phase transition from ablation to evaporation of PMMA irradiated by pulsed CO₂ laser devices to be used as reference data for Ultra-Conservative Minimally Invasive Surgery (UCMIS) with commercially available medical lasers. This step is important because it allows forecasting the micro boundary drilling conditions of a laser device implemented in Operating Room (OR) in conjunction to minimally invasive tools. The primary goals of reducing the invasive characters of an operation, and the associated risks of unwanted lateral tissue damage during surgery, are the key objectives of UCMIS protocols.

Background Data

Currently, the data available on literature do not report any guideline for a generic set-up configuration which produces the smallest ablations using non-Gaussian laser beams. This would help to further improve the overall quality of the UCMIS protocols via endoscopic scalpels to deliver minimal ablative energy. The Author has recently published a study on absolute UCMIS conditions.

Methods

The equation of the evaporation time has been used to identify the most effective and safest correlation amongst the following five magnitudes: output power W, focal length f, pulse width t_1b, beam TEM mode (M2 parameter) and the safest "not-to-exceed” radius of the allowed crater on the irradiated sample. The mathematical validation of this methodology is described and discussed.

Results

The optimized combination of these 5 magnitudes for a TEM₂₂ laser beam profile has been identified and it can be used for reference of UCMIS procedures using commercially available pulsed CO₂ lasers at the wavelength of 10.6 μm. The PMMA ablation temperature and the start of the evaporation phase can happen only starting from 354.5 degC or above. More investigations are needed to validate the whole procedure before any preliminary surgical utilization can be considered.

Keywords: PMMA; CO₂ Laser-Beams; CW; Output Power; Exposure Time; TEM; UCMIS Definition; Focal Length; Sublimated Volume, Evaporation Crater and Depth; LCA Algorithm

Abbreviations: UCMIS: Ultra Conservative Minimally Invasive Surgery; MIS: Minimally Invasive Surgery; OR: Operating Room

The Definition of UCMIS and Its Importance

Minimally Invasive Surgery (MIS) is a type of surgery aiming to minimize the size of surgical incisions. This type of surgery is performed using thin-needles combined to endoscopes to visually control the surgical operation via several smaller incisions rather than more radical and larger ones. The goal of minimally invasive surgery is to reduce postoperative pain, speed recovery, minimize blood loss, and lessen tissue scarring. The Ultra-Conservative MIS (UCMIS) is a type of MIS which aims to use the physically smallest incisions possible on a human tissue, still allowing the surgical treatment. The quantification of the overall conditions to geometrically reach these smallest possible injuries is mathematically determined by using several laws ofthermodynamic in conjunction to the physics of the laser beam interaction with the biological media being irradiated. Additionally, these minimal sizes are dependent on the type of surgical operation required case by case and on the type of exposed tissue. Reference values for generic UCMIS conditions are: W<0,7 Watt; crater diameter < 0,4 cm; t_1b < 0,01s.; evaporated mass per pulse < 0,01 gr. and crater depth < 0,2 cm (all data refer to PMMA) [1].

These concepts are important for both the industry and the surgeons communities: the first one can plan the design of future medical equipment based on the calculated physical limits intrinsically present in each operative procedure, while the latter can better foreseen the boundaries of a given surgical operation during the planning phase of the same and consequently better estimate the associated risks. UCMIS brings lots of new insights into both early thermodynamic and mechanical ablation phenomena associated to the smallest possible thermal injury and avoidable collateral complications [2]. Examples are the treatments, in orthopedic applications, of fine human bone structures, in neurology the micro dissection of nerves and in general surgery the generic treatment of other small anatomical structures as required case by case. In order to define a unified theory which addresses all the complex correlated thermodynamic phenomena taking place during the production of laser beam craters in low-water-content tissues, one key parameter to use as reference all the relevant optical coefficients of the PMMA at 10.6 μm.

Currently, the data available on literature do not report any numerical correlation amongst configurations of values which guarantee a safe CO₂ laser beam spot size with still surgical relevance. This must be in conjunction to minimal heath ablation with reduced side thermodynamic damage at 10.6 μm for generic combinations of output power in CW, non-Gaussian TEM mode, pulse width and focal length. The transition phase from ablation to evaporation must be discussed in detail [3]. The procedure to obtain these parameters would help to further improve the overall quality of UCMIS protocols via endoscopic scalpels. These use both mechanical focusing heads and fiber optic instrumentation to deliver ablative energy on tissue.

The focused lasers' spot size on any irradiated media is linearly depending on the focal length of the focusing head: this means that the volume of the ablated tissue is minimal if the focal length in use is he shortest possible one keeping the same output power [4]. The mathematical calculations to obtain the best combination of all the user-configurable parameters of a generic non-Gaussian medical laser device used for Ultra Conservative Minimally Invasive Surgery (UCMIS) procedures are here described. The same experimental set-up to validate the correctness of the LCA Algorithm has been published by the same Author several years ago (Appendix) is used in the present study also. The LCA algorithm is still an essential tool to determine the entire time-dependent coefficients linked to CO₂ laser beam ablation processes in PMMA. However, for the purposes of this Paper, it becomes also evident that in case of a generic combination of non-minimal laser parameters in output irradiating for a longer period of time, the pure evaporation processes of the irradiated media have here a much more important meaning.

In all the other limiting processes related to the minimal onset of the crater creation, the full process of combustion and evaporation cannot be observed; rather one can see the beginning phase of the ablative process only. This is caused by the very short-in-time temperature increase beyond the melting point but still below the evaporation threshold followed by full-blown combustion. This crucial difference has been described by other Authors also [1,2] most of polymers tend to ablate before evaporation. Normally, the heating of a substrate would lead to thermal expansion of a material and an explosivephase transition [1]. However, the high viscosity and cohesive energy of polymers greatly delays thethermal expansion and evaporation during the laser irradiation in both photochemical and photo thermalprocesses. It has been shown that the ablation of polymers starts when the density of broken bonds in the surface layer reaches a certain critical value [1]. The direct scission events, as in photochemicalprocesses, lead to modification of material and consequent reduction of molecular weight and cohesiveenergy of the polymer chain. However, the photochemical processes alone would require very highfluencies to increase the energy density and number of broken bonds [5].

For this reasons, ablation can be initiated at energies densities much lower than those required for vaporization due to the occurrence of Photo mechanical effects caused by laser- induced pressure build-up [1]. In order to solve the mathematical challenge associated to all these aspects, one has to start from the physics principles involved in non- limiting craters generation of polymers exposed to CO2 laser beams. These media, as known, well represent [4,6,7] the thermodynamic behaviors of low-water content biological media exposed to the same laser wavelength. The numerical value of the optical absorption coefficient has been kept constant throughout the entire mathematical calculation: α = 536.9 cm^-1. This parameter has been published already by the same Author [1] and it has been proven to be the correct value for PMMA [6].

From the Literature (2), we know that the evaporation time is given by:

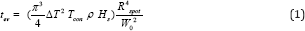
where ΔT is the PMMA evaporation temperature minus room temperature, T_con is its thermal conductivity, ρ is its density, Hs is its specific heat, Repot is the spot radius of the focal in use and W0 is the power in Watt irradiating the PMMA sample on the focal spot. The ablation and the evaporation times are closely linked : after a very short initial ablative-only phase (happening from 0 J/cm2 up to max. 7.17 J/cm² (4) and if the irradiation persists in time or in fluency beyond this upper limit of 7.17 J/cm2 , than the evaporation starts followed by combustion [7]. The existence of separate ablative and evaporative levels for polymers has been demonstrated by several Authors (1) already. In the past, it has been demonstrated that the time t_1b is linked to the on-set of ablation of the initial minimal volume (Appendix), therefore we can say that, using Equation 3, the Subsequent evaporation time ten is linked to t_1b via a small time margin δ as follows:

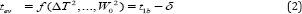
And therefore:

And finally, absorbing the minima δ into the function f, we can use the following derivation of Equation 3:

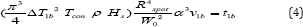
Where ΔT1b is the temperature after the on-set of evaporation, α is the absorption coefficient of PMMA at the wavelength of the CO₂ laser and v_1b is the minimal volume following LCA (Appendix). This formula regulates the conditions for the on-set of the minimal evaporation under UCMIS regime for any arbitrary focal length which is now, per definition, larger of the minimal one presented in (5). The ablation and the evaporation times are closely linked: after a very short initial ablative-only phase (happening from 0 J/cm² up to max. 7.17 J/cm² (4) and if the irradiation persists in time or in fluency beyond this upper limit of 7.17 J/cm² , than the evaporation starts followed by combustion. From Equation 3, 4 and 5 we can write:

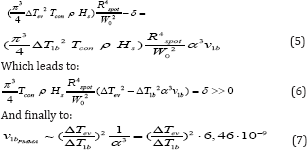
The published value (5) of the PMMA minimal ablated volume for f_c = 0,013” is:

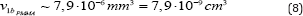
From Equation 6 and Equation 7 we then have for the same reference room temperature T₀ = 23 degC:

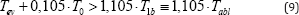
Numerically, from literature 14 we have ΔT_ab = 300 degC, therefore using Equation 21 we find ΔT_ev > 331.5 degC which is perfect agreement with other published results (1, 2, 13, 14). This entire Means: T_ab1= 323 degC and T_ev > 354.5 degC for PMMA exposed to CO₂ laser beam (Equation 21). In other words, the photo ablation happens at 323 degC, while the evaporation and subsequent combustion starts later, when the temperature reaches at least 354.5 degC. The interval between these two temperatures can be associated to the extra time delay needed for energy pile-up required to break the high viscosity and cohesive energy of break the high viscosity and cohesive energy of polymers break the high viscosity and cohesive energy of polymers and evaporation during the laser irradiation in both photo-chemical and photo-thermal processes [1].

The positive results from Equation 21 fully validate the proposed method based on the used Equations 4, 6, 7, 11, 12, 13, 15, 16 and 17, which are also physically and mathematically correct. This confirms also the methodology used for the smallest possible focal performances 5. As further mathematical proof of the correctness of the 354.5 degC as PMMA evaporation threshold, one can think to consider instead a higher or a lower value than this one. Then, these new values would be numerically positioned outside the tolerance limits of the presented calculations and outside also the thermodynamic uncertainties of the PMMA data reported in the Literature. This assumption would also imply the existence of a higher or a lower absolute minimal volume beyond the same tolerance limits of the model used to calculate the results of Equation 20: this is impossible per definition [5].

The Authors has demonstrated that ΔT_ev> 331.5 degC which is perfect agreement with other published results (1, 2, 13, 14). This entire means: T_ev = 323 deg C and T_abl > 354.5 degC degC for PMMA exposed to CO₂ laser beam (Equation 21). In other words, the photo ablation happens at 323 degC, while the evaporation and subsequent combustion starts later, when the temperature reaches at least 354.5 degC. The interval between these two temperatures can be associated to the extra time delay needed for energy pile- up required to break the high viscosity and cohesive energy of polymers. These ones greatly delay the crater expansion and evaporation during the laser irradiation in both photo-chemical and photo-thermal processes [1].

Also, the Author has presented and discussed the relationships between the main optical, thermodynamic and time-dependent parameters linked in the creation of the smallest possible crater dimensions in PMMA for a generic non-limiting laser beam device set-up irradiating TEM-dependent CO₂ laser beam profiles in pulsed mode. The mathematical demonstration of the correctness of the method used is also presented and discussed using the considerations about Equation 21. The focal 2” with TEM00 (underlined in bold) is the limit for UCMIS, therefore any focal lengths between [0, 05”-TEM33] and [2”-TEM00] can be used with any laser device set-up in surgical operations which need to satisfy UCMIS safe conditions for evaporation. The ablation rate as a function of laser fluency has been also investigated. It has been again demonstrated that the PMMA possesses two separate ablation and evaporation thresholds [1]. The first one [4] is below 7.17 J/cm² associated to low material removal rate due to ablation only.

The other threshold (even for W^min , [5] is between 16-19 J/cm² with a rapid Increase in the material removal rate due to evaporation followed by combustion. It is interesting to observe that the range 16-19 J/cm² is respected even by the not- acceptable focal: The reasons which makes them unacceptable must be found in parameters, such the evaporated volume and the total exposure time, which go beyond any mathematical and physical acceptance, such as evaporated volumes of several cubic centimeters and exposure time pulse width longer than 10s. The suggestion to obtain the best UCMIS results for generic CO₂ laser device using the combination of t0, τ R and t_1b in sequence is recommended for any focal lengths between [0,05”-TEM33] and [2”- EM00] which generate evaporation between 16 and 19 J/ cm² on the spot size. The presence and the combination of acceleration-, deceleration- and speed-related components in the early phase of the crater sublimation, and during single pulse duration, have been demonstrated. Further investigations are needed to completely validate the global procedure before adopting it in real-case surgical operations on living organisms.

In 1992, the Author has demonstrated [8] the existence of a very simple empirical law which allows to forecast the volume ablated by a CO2- TEM22 laser beam (M ² = 2 +1 = 5 )in PMMA and compact bone samples. The main equation combines several values of the focal length of the focusing head in use to the R (t) and Z (t) development curves of the crater diameter and depth versus the exposure time of the sample to the radiating beam. After comparing the geometrical details of several hundreds of craters in PMMA against focal lengths, TEM modes and beam widths of the laser beam, this fundamental equation can be written as follows:

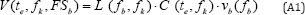
Where V(t_e,f_k, FS_b) is the resulting crater volume, f_k is the focal length in use, f_b is the basic focal length, F_Sb is the Focal Sequence of both fk and f_b, while te is the exposure time and v_b(f_b) is the basic ablated volume of F_Sb just after melting and prior to evaporation [9]. The following definitions have been introduced:

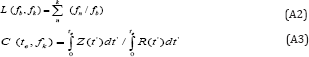
The FSb and fb are defined as follows (arrows indicate one or two examples out of all possibilities; unit length is 'inch'):

It has been demonstrated [10-12] that v_b = 97 .10^-4 mm³ is the correct constant value to be used to forecast all the PMMA crater volumes obtained for 10 Watt laser beam power and for all f_k , f_b and t_e used in that Study.

If we put V(t_e,f_k, FS_b) = v_b (f_b) in equation (A1), we obtain the basic equation

Which is the first step for any investigation about the starting phase of the ablation processes associated to a measurable and known geometrical shape and which [12-14] take place just before evaporation? Additionally, the following definitions have been used:

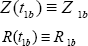
Recent investigations have pointed out to the following relation :

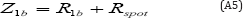
with a t_1b much higher than the one previously calculated. This critical value, associated to a transition of the dynamics of the crater production (acceleration of the horizon towards constant speed), leads to :

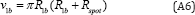
for the LCA Algorithm. More details about these new facts will be published by the Author soon.

1. PF Conforti, YG Yingling, BJ Garrison (2007) Computational studies of ultraviolet ablation of poly (methylmethacrylate). Journal of Physics: Conference Series 59: 322-327.
2. PW French, DP Hand, C Peters, GJ Shannon, P Byrd, et al. (1998) Investigation of the Nd:YAG laser percussion drilling process using high speed filming. Proc. Laser Material Processing Conference ICALEO 85(1): 1-10.
3. Peter Doyle, Curt McMullen (1989) Solving the quintic by iteration. Acta Mathematica 163(1): 151-180.
4. Canestri F (2011) Accurate quantification of the Optical Absorption Coefficient and of the Thermal Relaxation Time for PMMA and for low- water-content media during early ablation with CO₂ laser-beam at the wavelength of 10.6 mm. Photo medicine and Laser Surgery 29(1): 61-66.
5. Canestri F (2011) Ultra-conservative Minimally Invasive Surgery (UCMIS) with Pulsed Non-Gaussian CO2 Laser Beams Focused Through the Shortest Possible Focal Length. Photo medicine and Laser Surgery 29(11): 759-766.
6. Walsh JT (1989) Er: YAG Laser ablation of tissue: effect of pulse duration and tissue type on thermal damage. Las Surg Med 9(4): 314-326.
7. Whiting P, Dowden JM, Kapadia PD (1992). A one-dimensional mathematical model of laser induced thermal ablation of biological tissue. Las Med Science 7(1-4): 357-368.
8. Canestri F (1992) Proposal of a computerized algorithm for continuous- wave CO₂ Laser on-line control during orthopedic surgery. Int J Clin Mon Comp 9: 31-44.
9. Canestri F (1997) Proposal of a computerized algorithm for continuous wave CO₂ laser on-line control during orthopedic surgery. Int J Clin Mon Comp 14(3): 199-206.
10. Canestri F (1988) A proposed Clinica l Application of a Model of CO₂ Laser Radiation Induced Damage Craters. J Med Eng Techn 12(3): 112117.
11. (2005) Lasers and laser-related equipment-Test methods for laser beam widths, divergence angles and beam propagation ratios.
12. TF Johnston (1998) Beam propagation (M²) measurement made as easy as it gets: the four-cut method. Appl Opt 37(21): 4840.
13. Rodhes BT (1994) Burning rate and flame heat flux for PMMA in the cone Calorimeter. NIST-GCR-95-664.
14. Urecht L, Lippert T (2010) Photo ablation of Polymer Materials. Photochemistry and Photo physics of Polymer Materials. John Wiley and Sons Inc 14: 541-568.