Mathematical Model of Antibiotic Residues after Applying Poultry Manure to Soil Water Volume 3 - Issue 4

Bin Zhao*¹, Aibing Li¹, Lichun Liang¹ and Jinming Cao²

• ¹College of Science, Northwest A & F University, China
• ²School of Information and Mathematics, Yangtze University, China

Received: March 19, 2018;   Published: April 09, 2018

*Corresponding author: Bin Zhao, College of Science, Northwest Agriculture and Forestry University, Yangling, 712100, China

DOI: 10.26717/BJSTR.2018.03.000935

Abstract PDF

Manure composition emissions can be effected by soil water with the application of poultry manure. The vectors to represent the relationship between soil water characteristics and antibiotic were generated. A Semi-empirical Richards equation is employed to model the law of soil moisture while precise solutions of Richards equation obtained by using the (G ' / G ) - expansion method and the homogeneous balance method. Then mode l which involves several variables including soil moisture content, soil depth and timescales was assumed according to the exact solutions of Semi-empirical Richards equation. At least one antibiotic was detected in all the soil water and poultry manure samples. And it is worth noting that all of parameters or constants in this function expression were determined by these data.

Keywords: Antibiotic; Poultry manure; Richards Equation; Soil Moisture; The (G '/ G ) - Expansion Method

The large-scale and intensified development of livestock and poultry breeding has resulted in a large number of veterinary antibiotics being used in the aquaculture industry and increasing year by year. Accumulation of antibiotics in the organism. It is very low, after the body absorbs a small part, it undergoes metabolic reactions such as hydroxylation, cleavage, and glucuronidation to produce inactive products, and about 60% to 90% pass through feces as it is. Excretion of urine and excrement of livestock and poultry have undoubtedly become one of the main sources of environmental pollution by antibiotics. The drug design of antibiotics is mainly to kill pathogenic pathogens. Once they enter the environment, they will inevitably pose a potential threat to other organisms in the environment. Firstly, the resistant pathogenic bacteria or variant pathogens in livestock and poultry are produced and continuously released into the environment. Secondly, livestock and poultry continue to excrete these antibiotics or their metabolites into the environment, so that drug resistant pathogens and mutant pathogens in the environment are continuously generated.

Both of these in turn stimulated the producers to increase the dosage and renew the drug varieties, which resulted in a vicious circle of "drug-contaminated environment → emergence of drug-resistant or mutated pathogens → increased dosages → environmental pollution". Fertilization by poultry manure has shown an important variance in soil water chemical characteristics. The state for regional soil moisture reserve is the strategic storage of water resources in the district. The distribution of soil moisture directly affects the supply of groundwater resources, determines the amount of water, which is absorbed from the soil and evaporated by the earth's surface plants, plays a decisive factor for plants' productivity, and also is regarded as strategic factors influencing the ecological environment security, the economic development and the people's lives in arid and semi-arid areas [1].

Presence of antibiotic and soil water physicochemical properties played key roles in degradation of numerous molecules and other processing. Fertilization is the commonest managing agricultural soils, and for a long time, intensive farming appealed to fertilizer to increase yields. Then livestock and poultry excrement will constitute one of the main reasons for the non-point source pollution of antibiotics in China. Therefore, based on the research results in recent years, combining the use of antibiotics in the livestock and poultry industry and the status of residues, this paper analyzes the fate and environmental risks of livestock and poultry excrement in soil, and puts forward the corresponding mathematical model. Darcy law is a fundamental theoretical method to describe the motion law of soil moisture, therefore a variety of Richards equations are deduced. For the nonlinear partial differential equations, the previous research method is to discuss their definite solutions and we commonly can acquire their numerical solution through the numerical method.

Whether the analytical solution of Richards's equations, which describes the change of soil moisture content with the change of time and space position in Darcy's law, has been the expectation, If we substitute some empirical representations of hydraulic conductivity and water diffusivity into Richards equations, the exact solution of Richards’s equation on soil moisture content, soil depth and time is of great significance. Furthermore, the greater parts of antibiotic were found in the soil water by poultry manure. In the past few years, many powerful methods to construct exact solutions of nonlinear evolution equations have been established and developed such as the homogeneous balance method [2-4], the (G ' / G ) -expansion method [5,6], the exp-function method [7,8] and so on.

One of the most effective and direct methods for constructing exact solutions of nonlinear differential equations is the (G ' / G ) - expansion method. The (G' / G) - expansion method, first introduced by Wang et al. [5], has been widely used to search for various exact solutions of NLEEs [9-11]. The (G'/ G) - expansion method is based on the [12,13] explicit linearization of nonlinear differential equations for traveling waves with a certain substitution which leads to a second-order differential equation with constant coefficients [14-16]. Finding an exact solution for Richards equation, by using the (G ' / G ) - expansion method, is the main goal of the present study.

First of all, we introduce a form of Richards's equations as follows:

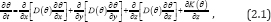
where D(θ) denotes water diffusivity; K(θ) denotes hydraulic conductivity; t denotes time; θ denotes soil moisture content; x,y,z denote coordinate axes. If the soil moisture content is lower than the saturated (unsaturated) moisture content with little change, we take as D(θ) = α, where α is a constant.

Many researchers have committed themselves to estimating soil hydraulic conductivity, as a result, various empirical representations of hydraulic conductivity are proposed. We assume that [12,13] unsaturated hydraulic conductivity is calculated by using the Libardi method, that is

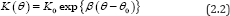
Where β is a constant; K₀ and θ₀ are the values of K and θ during steady-state infiltration, respectively.

Next, we have intend to simplify equation (2.1), in other words, here we only consider the case that soil moisture flows in the vertical direction, and therefore we have

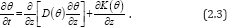
By substituting D(θ) = α and equation (2.2) into equation (2.3),hence the following semi-empirical Richards equation is obtained:

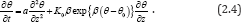
In this section, by make use of the (G' / G) -expansion method, we obtain an exact solution for the equation (2.4), however, we omit the description of the (G' / G) -expansion method. If you are interested in this method, you can refer to the reference [4].

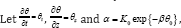then the equation (2.4) can be equivalently changed into

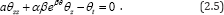
Using the travelling wave variable θ(z, t ) = θ(ξ) and ξ = z — ωt carries out the equation (2.5) into an ordinary differential equation for θ = θ(ξ)

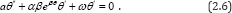
In order to apply the (G' / G) -expansion method, we use the Painleve transformation 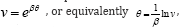, hence the equation (2.6) can be written as

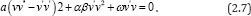
Suppose that the solution of ordinary differential equation (2.7) can be expressed by a polynomial in (G' / G) as follows:

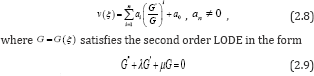
where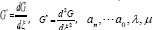are real constants to be determined later.

According to the (G ' / G ) - expansion method, considering the homogeneous balance between vv'' and v'v² in the equation (2.7), we get 3n +1 = 2n + 2 ࠶ n = 1 , hence we can write (2.8) as

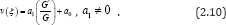
Substituting (2.10) along with (2.9) into (2.7) and collecting all terms with the same order of 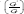together, the left-hand side of (2.7) are converted into polynomial in 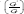. Setting each coefficient of each polynomial to zero, we derive a set of algebraic equations for λ,μ,ω,α₀, α,₁ as follows:

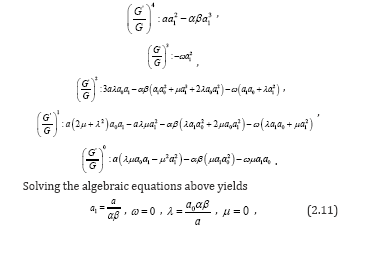
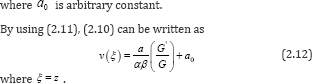
Substituting the general solutions of equation (2.9) into (2.12), we have an exact solution of the equation (2.7) as follows:

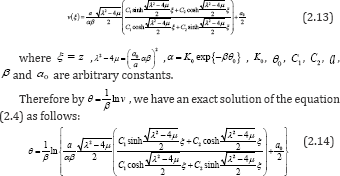
According to what has been discussed above, we assume that soil moisture content, soil depth and time satisfy

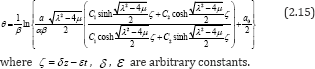
Data used here were collected during an internal drainage experiment, carried out on a sandy-loam Red Yellow Latosol (Typic Hapludox) of the county of Piracicaba, SP, Brazil, with a fairly homogeneous profile down to the depth of 2m [17]. They consist of soil water content values calculated from tensiometer readings, through the use of laboratory established soil water retention curves and of soil water potential heads, measured with the same mercury manometer tensiometers. The soil water retention curves were established by drying wet samples, to minimise hysteresis effects. Data are averages of 3 replicates collected during the internal drainage of three 3 m by 3m plots, 10m apart, previously submitted to infiltration by ponding water on the soil surface until quasi-steady flow. To prevent evaporation losses, the soil surface Table 1: The soil profile characterization. was covered with a plastic sheet during the drainage process, so that all conditions stated in Libardi et al. [12] were met [18]. Soil- water retention curve at each soil depth was determined using undisturbed samples (45mm diameter by 45 mm height) on porous plate funnels (matric potential head h from 0.26m to 1.87m) and porous plate pressure cells (matric potential head h from 3.0 m to 8.0m).

Soil bulk densities were also determined using volumetric cylinders of 45mm diameter and 45mm height. Table 2 also presents the obtained values of parameters a, m, n, r, and the equation of Van Genuchten [19] as well as their r2 values; soil water content values during the redistribution time were obtained by means of these equations. The saturated soil water contents 0 were also taken from the Van Genuchenten equation for matric potential h=0. The determination of 0 in the field at steady infiltration is practically impossible, except with neutron probes, which have to be well calibrated and present difficulties for measurements close to the soil surface. It is important to note that it is difficult to fully saturate a soil profile in the field and that; therefore, field values of 0 are, in general, slightly lower than those measured in the laboratory. Tables 2 and 3 present the average raw data of soil water content and matric potential head, which are presented here for any other development of soil water movement theories. Soil water potential head H (cm of water) is considered as the sum of the gravitational head z and the matric potential head h [17].

In this model, the data were collected during an internal drainage experiment, which was carried out on a sandy-loam Red Yellow Latosol (Typic Hapludox) of the county of Piracicaba [17]. We use the data to determine the parameters in the identity (2.15), and therefore the predicted values of soil moisture content are calculated from (2.15). From data in (Tables 1&2), it revealed that volumetric soil water contents (m3/m3), for different redistribution times (t) and different depths (z). And the parameters of equation (2.15) for each time and soil depth were determined by using data fitting method. All of these can be seen in Table l.These parameters are shown in Table 3. From these parameters, we obtain a function express in which soil water content is independent variable whereas time and soil depth are two dependent variables.

Table 1: The soil profile characterization.

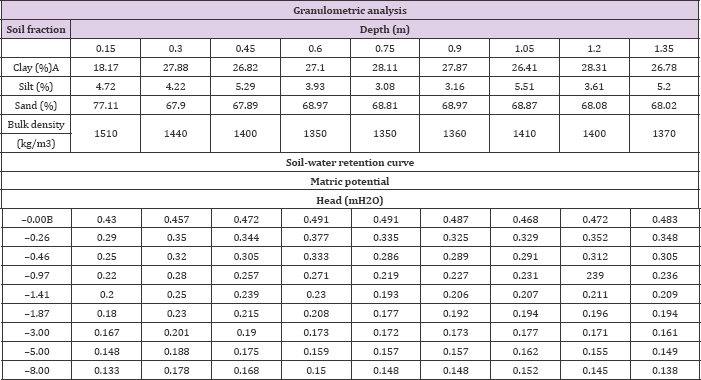
Table 2: Volumetric soil water contents θ (m³/m³), for different redistribution times (t) and different depths (z).

Table 3: Parameters of equation (2.15).

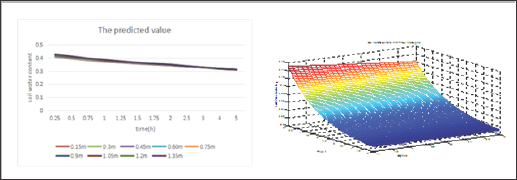
And thus the predicted values of soil moisture content are also presented in (Table 4) according to equation (2.15). Compared with the actual values, the mean squared error (MSE) is 0.00077423, which suggests that equation (2.15) describes the changes of soil water content with the time and soil depth very well. According to Table 2, the following Figure 1 can be presented. Figure 2 show that equation (2.15) has the same tendency with the Figure 1. Although the contents are not equal at the range of 0-14m, it can be recorded as the same contents duo to little change in this range. Since the hypothesis that the water diffusivity is constant, Figure 2 obviously conforms to the actual situation.

Table 4: The predicted values.

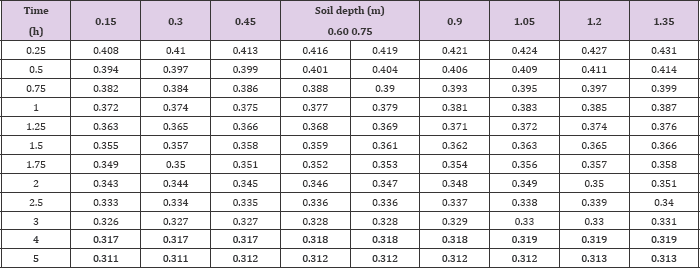
Figure 1: Original figure.

Figure 2: The smoothed figure.

We propose a new model equation (2.15), which describes the changes of soil water content with the time and soil depth, by finding out an exact solution of equation (2.4) through currently prevalent (G' /G) -expansion method. Even though equation (2.15) is established with the assumptions that the hydraulic conductivity satisfies exponential function and water diffusivity is a constant, to some extent, the very low mean squared error (MSE) indicates that equation (2.15) is a great reflection in change of soil water content with the time and soil depth. However, the simple assumption of water diffusivity might incur larger error in term of actual values of soil water content, thus a precise empirical representation of water diffusivity is expected to be proposed. With the rapid development of science and technology, the solutions to nonlinear differential equations would be enriched, and more excellent results on Darcy's law might be acquired. All these results also suggest that soil water play a considerable role in the fate of antibiotic in the environment. Further research is needed to give the detection of antibiotic from animal manure in soil water by the regression equations constructed in the present study.

This work was supported by the Fundamental Research Funds for the Central Universities (2014YB030), Ministry of Education and State Administration of Foreign Experts Affairs "Overseas Teacher" project (MS2011XBNL057), the Key Construction Program (2015SD0018) of International Cooperation Base in S&T, Shaanxi Province, China.

1. (2016) Cancer Moonshot Blue Ribbon Panel Report.
2. Weintraub H, Izant J, Harland R (1985) Antisense RNA as a molecular tool for geneti analysis. Trends in Genetics 1(1): 23-25.
3. Dervan PB (1992) Reagents for the site-specific cleavage of megabase DNA. Nature 359: 87-88.
4. Trojan J, Johnson T, Rudin S, Ilan Ju, Tykocinski M, et al. (1993) Treatment and prevention of rat glioblastoma by immugenic C6 cells expressing antisense insulin-like growth factor I RNA. Science 259: 94-97.
5. (1990) Wikipedia-Encyclopedia. Gene Therapy History.
6. Daughaday WH, Rotwein P (1989) Insulin-Like Growth Factors I and II. Peptide, messenger ribonucleic acid and gene structures, serum, and tissue concentrations. Endocrin Rev 10(1): 68-91.
7. Trojan J, Pan YX, Wei MX, Ly A, Shevelev A, et al. (2012) Methodology for anti-gene anti- IGF-I therapy of malignant tumours. Chemother Res Pract 12.
8. Trojan A, Ly A, Wei MX , Pan YX , Kopinski P, et al. (2017) Experimental and clinical anti - gene anti IGF-I therapy. In J Trojan (Eds.), Cancer immunogene therapy. Anti- gene anti IGF-I approach. Case of glioblastoma. (Edn.). Lambert Academic Publishers, Germany 3: 68-91.
9. Wongkajornsilp A, Ouyprasertkul M, Sangruchi T, Huabprasert S, Pan YX, et al. (2001) The analysis of peri-tumor, necrosis following the subcutaneous implantation of autologous tumor cell transfected with an episome transcribing an antisense insulin-like growth factor 1 RNA in a glioblastoma multiforme subject. J Med Assoc Thai 84(3): 740-747.
10. Popiela T, Sierzega M, Gach T, Jarocki P, Trojan J (2003) Phase I trial of colorectal cancer immunotherapy using autologous cancer cells transfected with an IGF-I antisense plasmid. Acta Chirurg Belg 5(103): 2-3.
11. Zhu C, Trabado S, Fan Y, Trojan J, Lone YC, et al. (2015) Characterization of effector components from the humoral and cellular immune response stimulated by melanoma cells exhibiting modified IGF-1 expression. Biomed & Pharmacother 70: 53-57.
12. Trojan J (2016) Anti-Gene anti IGF-I technology applied for cancer immunotherapy. World J Res Rev 1(3): 67-75.
13. Castillo T, Trojan A, Noguera MC, Jay ML, Crane C, et al. (2016) Epistemiologic experience in elaboration of molecular biology technology for immunogene therapy (in Spanish)Rev Cien 2(25).