Abstract
The mercurimetric titration of chloride with sodium nitroprusside used as indicator, is formulated. A systematic error involved, with location of the end point of titration is calculated at different concentrations of components in the system tested. The results of calculations, obtained with use of a computer program, are presented graphically.
Keywords: Chloride determination; Mercurimetric titration; Sodium nitroprusside; Systematic error
Introduction
A titration procedure aims to determine the concentration of a solute in a solution tested, in presence of an indicator used for registration of the end point (e) of the titration. For example, Cl-1 ions are determined in Mohr’s method by titration with AgNO3 standard solution, in presence of K2CrO4 in the titrand [1-3]; the end point is indicated here by the Ag2CrO4 precipitate. In the Liebig method of cyanide determination, KCN solution is titrated with AgNO3 solution; the end point is indicated here by AgCN precipitate [4,5], as auto-indicating species. In the Denigès’ modification of the Liebig titration, the solution of KCN + KI + NH3 is titrated with AgNO3 solution; the end point is indicated here by the AgI precipitate [4,6]. Systematic error of the analyses was evaluated from calculations made on the basis of charge and concentration balances, and all thermodynamic knowledge expressed by equilibrium constants for the species related to the systems in question.
The present paper gives an evaluation of systematic error in mercurimetric titration of chloride in presence of sodium nitroprusside Na2Fe(CN)5NO⋅2H2O as indicator [7-10]. The nitroprusside ions, Fe(CN)5NO-2, form a white precipitate of HgFe(CN)5NO [11,12]. The titration is performed at pH = 1.5 – 2 [13].
Here and in further parts of this paper, the charges zi of the
corresponding species 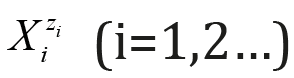 are omitted, when written in
terms of molar concentrations, i.e., the notation [Xi] is applied here,
for simplicity.
are omitted, when written in
terms of molar concentrations, i.e., the notation [Xi] is applied here,
for simplicity.
Some preliminary remarks
The system considered is an example of electrolytic non-redox system. The electrolytic non-redox (and redox too) systems can be considered according to GATES principles [14], if all
(i) qualitative (specification of components forming a system, and species in the system thus formed),
(ii) qualitative (concentration of components), and
(iii) physicochemical (thermodynamic equilibrium constants) is available. Any non-redox system is formulated with use of charge and concentration balances, and complete set of expressions for equilibrium constants. Charge balance involves charged species of a system.
The set of concentration balances involves relations between concentrations of components and species, formulated – separately – for particular elements or cores ≠ H, O. For a redox system, the set of elemental balances is completed by Generalized Electron Balance (GEB), formulated on the basis of the 2f(O) – f(H) balance [15], within GATES/GEB. Some examples of redox systems were presented also in this Journal [16].
Static and dynamic electrolytic systems are distinguished. A dynamic system is realized in titration, where V mL of titrant T is added into V0 mL of titrand D, and V0+V mL of D+T mixture is obtained at defined point of the titration [17]. Concentrations of solutes (a) in D are denoted by C0 (for analyte), C01, C02, …, and (b) in T by C (for reagent), C, C2, …. In the reference system considered here, Hg(NO3)2 (C) is the reagent, NaCl (C0) is the analyte, Na2Fe(CN)5NO⋅2H2 (C01) is the indicator. Moreover, HNO3 (C1) is the component in T that prevents precipitation of HgO when Hg(NO3)2 solution is prepared as T.
Within GATES there are considered, among others, the systems in which a solid phase is formed. Examples of this kind are provided e.g. in [6]. There may also be a change in the solid phase composition, see e.g. [18].
The results of calculations preformed according to GATES principles with use of iterative computer programs [14], can be presented graphically on the related 2D diagrams, where the fraction titrated

is marked on the abscissa, as an independent variable, where C and C0 are expressed in mol/L, V and V0 in mL. This is the simple way to normalize the respective graphs, i.e., the independence of their shape from the V0 value.
The Φ plays also the key role in formulation of Generalized Equivalence Mass (GEM) concept [19], compatible with GATES principles. Within GEM formulation, the end (e) and equivalence (eq) points are related to the titration curve. At the end point, the visual titration is terminated, when indicated by a desired/ pre-assumed color change of the D+T mixture, or by the first appearance of a solid phase, e.g. AgI in the Liebig-Denigès method [6], or HgFe(CN)5NO in the titration considered here. Turbidity in D+T provides the appropriate indicator (indicating component), e.g., KI in the Liebig-Denigès method, or Na2Fe(CN)5NO⋅2H2O in the method discussed here.
Equation (1) can be rewritten as follows

As we see, the fraction V/Φ value is constant during the titration in D+T system; it depends only on the pre-assumed/ imposed values for C, C0 (intensive quantities) and V0 From Eq. (2) it follows that V/Φ takes the same value at the end (e) and equivalent (eq) points, i.e.,
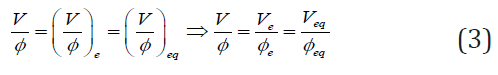
We have

where mA [g] and MA [g/mol] denote mass and molar mass of the analyte (A), respectively. From Equations (1) and (4) it follows that

From (3) and (5) one obtains:

However, Eq. (5a) cannot be applied for the evaluation of mA (Ve known, Φe unknown). Also, Eq. (5b) is useless (the “rounded” Φeq value is known exactly, but Veq is unknown), as Ve (not Veq) in visual titrations is determined experimentally.
Because the Equations (5a) and (5b) are inapplicable, the third, approximate formula for mA has to be applied, namely:
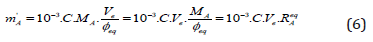
where Φeq is put for Φe in Eq. (5a), and
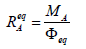 (7)
(7)is named as the equivalent mass of the analyte A. The relative error in accuracy resulting from this substitution equals to
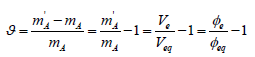 (8)
(8)For Φe = Φeq one gets ϑ = 0 and m'A = mA; thus Φe≅ Φeq, i.e. Ve ≅ Veq corresponds to m'A = mA
A conscious choice of an indicator and its color change during the titration is possible on the basis of analysis of the related titration curve. In particular, at Φeq=1/2 we have ϑ = 2φe −1. The ϑ values are usually expressed in %.
The numerical values for Φe are usually close to Φeq values expressed by a ratio of small natural numbers [19]. For example, in the system considered here we have Φeq = 1/2. The difference Φe- Φeq , when compared with the uncertainty of Φ value, is acceptable from the one-drop error viewpoint when |Φe- Φeq | < 0.003 [19].
Calculation procedure
The calculation specified below differs significantly from the one usually practiced in GATES, where a complete set of independent balances and equilibrium constants is applied. In particular, the GATES procedure can be applied to the model D+T system with NaCl (C0) + Na2Fe(CN)5NO⋅2H2O (C01) as titrand D (V0), and Hg(NO3)2 (C) + HNO3 (C1) as titrant T (V). However, the mercurimetric titration is applied also for the chloride samples from more complex media, where composition of a sample matrix is undefined [20]. Some kinds of the samples were also tested in clinical laboratories, e.g. [21]. Other indicators were also applied for this purpose, see [22].
In the simplified calculation procedure, charge balance and other concentration balances (except for Cl and Hg, and nitroprusside) are omitted. The concentration balances are confined to monophase system, including the end (e) point, i.e. the first point of the titration, where the solubility product (Ksp = [Hg][Fe(CN)5NO], pKsp = 8.6) of HgFe(CN)5NO is valid.
From concentration balances for Cl and Hg:

we have, by turns,

i.e., the fraction titrated (Eq. 1) has the form
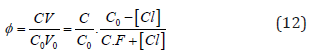
where

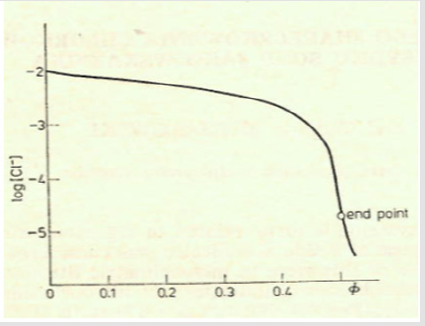
and [Hg(OH)i] = KiOH [Hg][OH]i (i=1,2, log KiOH = 10.3, 21.7), [HgCli] = KiCl[Hg][Cl]i (i=1,2,3,4; log KiCl = 6.74, 13.22, 14.07, 15.07). The pCl = – log[Cl] vs Φ dependence, obtained from Equations (12) and (13), is considered as titration curve, and presented in Figure 1. It should be noted that the jump on this curve occurs in close vicinity of the fraction titrated value Φ = Φeq= 1/2.
Figure 1: The titration curve for mercurimetric titration of chloride at C0 = 0.01, C01 = 0.003, C = 0.1.
A detailed discussion on the balances (9), (10) leads to conclusion that at the vicinity of the end (e) point, pCl ≈ 4.7, [Hg(OH)2] ≪ [HgOH] ≪ [Hg] ≪ [HgCl] < [HgCl2] ≫ [HgCl3] ≫ [HgCl4], it can be simplified into the form
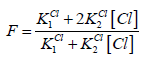 (14)
(14)Let V = Ve denotes the volume of titrant where the solubility product Ksp of HgFe(CN)5NO is attained. Assuming that nitroprusside ion does not form protonated species [23], at V = Ve we have:
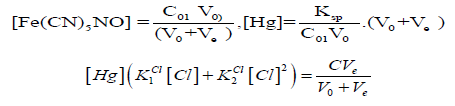
and then

If [Cl] ≪ C⋅F , at V = Ve, from Equations (12) and (14) we have
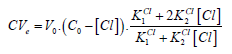 (16)
(16)From Equations (15) and (16) we have the equation
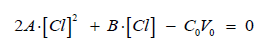
where
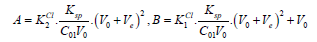
Then we have
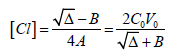 (17)
(17)where
Δ = B2 + 8A⋅C0V0
Setting (17) into (15) gives the equation
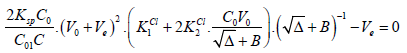 (18)
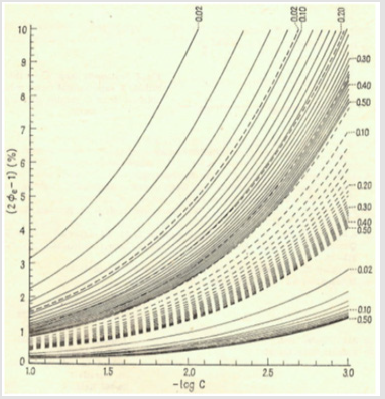
(18)The Ve value can be found from Equation (18) according to zeroing procedure, realized with use of a computer program for particular V0, C, C0, C01, Ksp, K1Cl and K2Cl values, considered as parameters of this equation. Then the relative systematic error involved with mass of chloride determination will be calculated in accordance with the principles of Generalized Equivalence Mass (GEM) formulation [19,24], and illustrated in Figure 2.
Figure 2: The 2 Φe-1 (in %) vs. –logC dependences plotted at different q = C0/C values; 0.02, 0.04, …. , 0.48, 0.50 at
a) C01 = 0.01 (lower continuous lines)
b) C01 = 0.003 (dotted lines)
c) C01 = 0.001 (upper continuous lines); the numbers on right side and at the top of the figure indicate the corresponding q-values.
Final Comments
The paper provides an example of application of physicochemical (thermodynamic) knowledge involved with gaining the information involved with expected systematic error of analyses made at different concentrations of NaCl (C0), Na2Fe(CN)5NO⋅2H2O (C01) and Hg(NO3)2 (C). Generally, at given C value, the error of chloride analysis grows with a decrease of C0 and C01 values, as indicated in Figure 2.
References
- Meija J, Michałowska Kaczmarczyk AM, Michałowski T (2016) Mohr’s method challenge. Analytical and Bioanalytical Chemistry 408(7): 1721- 1722.
- J, Michałowska Kaczmarczyk AM, Michałowski T (2016) Solution to Mohr’s method challenge. Analytical and Bioanalytical Chemistry 408(17): 4469-4471.
- Michałowska Kaczmarczyk AM, Spórna Kucab A, Michałowski T (2017) Solubility products and solubility concepts, in: Descriptive Inorganic Chemistry. Researches of Metal Compounds. In: Akitsu T (Ed.), InTech Chap 5: 93-134.
- Michałowski T (1983) An error of Liebig-Denigès’ method of determination of the cyanide. Chemia Analityczna 28: 313-315.
- Michałowski T, Wajda N, Janecki D (1996) Unified Quantitative Approach to Electrolytic Systems. Chemia Analityczna (Warsaw) 41: 667-685.
- Michałowski T, Asuero AG, Ponikvar Svet M, Toporek M, Pietrzyk A, et al. (2012) Principles of computer programming applied to simulated pH–static titration of cyanide according to a modified Liebig-Denigès method. Journal of Solution Chemistry 41(7): 1224-1239.
- Votoček E (1918) Ueber ein neues Titrierverfahren für Cl, Br, CN und Hg (About a new titration method for Cl, Br, CN and Hg). Chemiker-Zeitung 42: 257-260.
- Schales O, Schales SS (1941) A simple and accurate method for the determination of chloride in biological fluids. Journal of Biological Chemistry 140: 879-884.
- Bernshtein VN, Belikov VG (1961) Sodium nitroprusside and its use in analysis (in Russian). Russian Chemical Reviews (Успехи Химии) 30(4): 532-549.
- Mázor L (1975) Analytical Chemistry of Organic Halogen Compounds, Pergamon Press Ltd, Oxford.
- Kolthoff IM, Sandell EM, Meehan EJ, Bruckenstein S (1969) Quantitative chemical analysis. In Kolthoff IM, Sandell EM, Meehan EJ, Bruckenstein S (Eds.), (4th edn.). The Macmillan Comp, London 743: 813-815.
- Cano A, Osiry H, Reguera L, Lemus-Santana AA, Reguera E (2015) Mercury(II) nitroprusside: A framework with an unusual topology. Journal of Solid-State Chemistry 225: 315-320
- Bishop E (1972) Indicators. Pergamon Press, Oxford.
- Michałowski T (2011) Application of GATES and MATLAB for Resolution of Equilibrium, Metastable and Non-Equilibrium Electrolytic Systems in: Applications of MATLAB in Science and Engineering, by Michałowski T (Ed.), InTech - Open Access publisher in the fields of Science, Technology and Medicine 1: 1-34.
- Michałowska Kaczmarczyk AM, Spórna-Kucab A, Michałowski T (2017) Generalized Electron Balance (GEB) as the Law of Nature in Electrolytic Redox Systems, in: Redox: Principles and Advanced Applications, Ali Khalid MA (Ed.) InTech 2: 9-55.
- Michałowska-Kaczmarczyk AM, Michałowski T (2018) The distinguishing role of 2⋅f(O) – f(H) in electrolytic systems. Biomedical Journal of Scientific & Technical Research 8(1): 1-10
- Michałowska Kaczmarczyk AM, Spórna-Kucab A, Michałowski T (2017) Principles of Titrimetric Analyses According to Generalized Approach to Electrolytic Systems (GATES). In: Advances in Titration Techniques, Vu Dang Hoang (Ed.), InTech 5: 133-171.
- Michałowski T, Pietrzyk A (2006) A thermodynamic study of struvite+water system Talanta 68(3): 594-601.
- Michałowski T, Pietrzyk A, Ponikvar-Svet M, Rymanowski M (2010) The Generalized Approach to Electrolytic Systems: II. The Generalized Equivalent Mass (GEM) Concept. Critical Reviews in Analytical Chemistry 40(1): 17-29.
- Labhade SR (2017) Selective mercurimetric titration assay of chlorine concentration in the water of green coconuts using novel indicator system. International Journal of Pharmacy and Pharmaceutical Sciences, 9(3): 268-272.
- Freiberger NA, Tellor KB, Stevens AM (2016) Comparison of Clevidipine Versus Sodium Nitroprusside for the Treatment of Postoperative Hypertension in Cardiac Surgery Patients. Hospital Pharmacy 51(6): 461-467.
- Roberts I (1936) Titration of Chloride Ion with Mercuric Nitrate Solutions Using Diphenyl Carbazide Indicator. Industrial & Engineering Chemistry Analytical Edition 8(5): 365-367.
- Wilson CL, Wilson DW (1960) Comprehensive Analytical Chemistry. Elsevier, Amsterdam 1b:74.
- Michałowska-Kaczmarczyk AM, Spórna-Kucab A, Michałowski T (2017) Principles of Titrimetric Analyses According to Generalized Approach to Electrolytic Systems (GATES). In: Advances in Titration Techniques, Vu Dang Hoang (Ed.), InTech 5: 133-171.
- Mercuric nitrate solution.
- Solubility Product Constants Ksp at 25°C.

 Mini Review
Mini Review