Abstract
The COVID-19 pandemic, caused by the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), is already the most worrying health problem worldwide. The virus spread rapidly across the countries, making many researchers looking for answers to mitigate the disease’s effects. While vaccines are not available on a large scale, mathematical modeling has allowed the scientific community to perform forecasts for decision-making and social distancing policies to decrease the velocity of the COVID-19 transmission. However, dynamic models must represent the pandemic’s reality considering validation criteria and an appropriate procedure that ensures realistic simulations. These principles are the only way to make an epidemiological model useful for studying and analyzing practical effects. From a control theory point of view, representative models ensure optimal solutions and allow a more reliable and robust control strategy. Therefore, this paper proposes a parameter identification algorithm for a dynamic pandemic disease model spread, including a new time-varying parameter for control applications. The developed framework uses an epidemiological model, denoted here as , capable of associating the real pandemic dynamics to its biological parameters and the population social mobility in real-time, which can be led by an appropriate optimal control strategy. Simulations and forecasts are performed comparing with official data of the epidemic in the United States.
Keywords: Covid-19; Epidemiological Model; Identification; Simulation; Control; Social Distance
Introduction
The COVID-19 pandemic is indeed the most severe problem in terms of public health of the last hundred years in the world. The first disease case caused by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) was reported in Wuhan (Hubei province), China, in December 2019 [1]. The virus spread rapidly across the countries, making Europe the epicenter of the epidemic in March 2020 and reaching North and South America, especially the United States and Brazil, killing millions of people. Since the World Health Organization (WHO) declared an international emergency on January 31, 2020, many researchers have been mobilized to find answers to mitigate the effects of the COVID-19. Although professionals well know this type of subject from the health area [2,3], other different scientific communities from mathematics, physics, and engineering have proposed strategies of forecasts, decision-making, and social distancing to decrease the velocity of the disease transmission [4-6]. In this context, the art of mathematical modeling [7] appears as an efficient technique to analyze and develop practical solutions for dynamic systems like an epidemic. The first mathematical model on theoretical epidemiology was proposed by Kermack and McKendrick [8] whose differential equations can represent the dynamics of susceptible (not yet infected with the disease) individuals, the number of active infected, and the individuals that are recovered and became immune to the virus. Known as the SIR model, researchers have used its properties and structure to describe the COVID-19 epidemic. In the work of Wu et al. [9], the SIR model was used to analyze the real transmission and death dynamics of the coronavirus in Wuhan, China. Furthermore, official data were employed in the model to estimate clinical severity and risks, which could support public health decision-making. Postnikov [10] demonstrated that the SIR model could be simplified to a logistic function in which simulation results presented good accuracy with real data. This model is applied in different forecast scenarios for India’s current epidemic and four of its cities, as presented by Malavika et al. [11].
Nevertheless, equivalent models and expansions of the SIR model are used in epidemiological studies for COVID19. Annas et al. [12] analyzed the stability and simulated outlines in Indonesia using a SEIR model and considering the epidemic effects due to isolation and vaccine. Rajagopal et al. [13] proposed a SEIRD model with fractional derivatives to represent the disease in Italy and predict the outbreak’s peaks, in which the authors base the results on real data. Thus, as classes of individuals, dynamic parameters, and intervention measures are included, these extended models became more complex [14-16]. Besides, other types of model which use signals and time series, deterministic and stochastic approaches can be found in the literature [17-19]. It is clear that these models are indispensable to understand the epidemic dynamics in order to avoid new infection and death cases, and promote governmental policies which enhance recovered individuals and decrease the negative effects of the COVID-19. However, validation procedures are required to use the models in practice. Generally, the recent literature has presented COVID-19 epidemiological models with incomplete validation criteria or numerical algorithms which deteriorate the real parameters. On the other hand, the epidemiological models that represent realistic scenarios guarantee practical and feasible solutions. Hence, in particular, engineering applications such as simulation [20], design [21], education [22], optimization and control [23] bring us an important perspective to face this terrible disease. Since few vaccines are previewed to be available to the people, especially in developing nations, social distancing is a fundamental method adopted by the governors to opposite the pandemic spread. The intention is to lower the probability of the virus transmission and slow the number of infected people. Flattening the curve of active infected prevents the collapse of the health systems caused by numerous patients with COVID-19 being treated and contributes to preventing the disease spread. The critical matter is when applying the social distancing and for how long. In this sense, the control engineering aided by epidemiological models can determine strategies of social distancing that balance health and economic aspects [24-27]. For this, a social distancing variable has to be incorporated into the epidemiological models. Based on the preceding, an identification algorithm for epidemic control is proposed in this work. The procedure is composed of two layers: the first one uses a discrete analytical equation to calculate the exact parameters which represent the system dynamics, and the second one, employing an optimization formulation used as a slight adjustment, approximates as closely as possible the epidemic curves to the real data, aiming to fit the dynamic model. Moreover, a social distancing variable is incorporated into the algorithm to relate its real effects on the epidemic, allowing proper predictions and investigation for control strategies.
The paper is organized as follows: in Section 2, the proposed parametric identification algorithm is explained in detail using the adapted SIRD + Ψ model structure. In Section 3, the model identification is performed, validated, and applied to simulate scenarios in the United States at different periods of the COVID-19 pandemic. In Section 4, a perspective and design of optimal control techniques that could be employed using the epidemiological model to mitigate the pandemic are approached; and the conclusions are stated in Section 5.
The Structure Model and Algorithm Description
The Susceptible-Infected-Recovered-Deceased (SIRD) model is used in this work since its equations are able to adequately describe the dynamic behavior of the SARS-CoV-2 [28,29]. As shown in the following, a dynamic variable representing the social distancing responses due to isolation policies is included in the model, denoted as SIRD+ψ.
Epidemiological Model
The SIRD model examined in this paper describes the dynamics of a population divided into compartments of susceptible (S) and symptomatic (reported) infections (I). The reported infections may present moderate to severe symptoms and, after the infection period, individuals may recover (R) from the disease or, in severe cases, result in death (D).
Thus, the SIRD+ψ model is expressed by the following nonlinear differential equations:
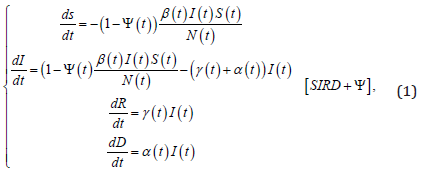
wherein the parameter β (t ) is the transmission rate; γ (t ) is the recovery rate, removing some individuals from the infected class, and the parameter α (t ) denotes the observed mortality rate of the virus. Social distancing index caused by mobility reduction measures is expressed by ψ (t ) , denoting restrictions on the circulating of people, i.e., Ψ(t ) =1 stands for a complete lockdown, whereas ψ (t ) = 0 means no social distancing. Note that these parameters may not be constant and may vary according to the stage of the pandemic. It is reasonable to think that, in the case of the virus does not mutate, the identified disease parameters tend to stabilize at a natural point. However, new events, such as changes in medical treatments or new government protocols, can affect the disease dynamic and consequently modify the SIRD parameters.
The size of the total population exposed is denoted by N (t )
and, in this work, it is assumed that natural deaths balance the
newborns; which holds that 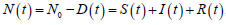 ,
wherein 0 N is the initial population size (before the contagion).
Moreover, the term β (t ) I (t ) / N (t ) represents the average number
of contacts that is sufficient for viral transmission from one
susceptible individual, per unit of time. Also, β (t ) I (t ) / N (t ) S (t )
counts as the total number of new cases from the number of
susceptible individuals, per unit of time. Another essential
information in epidemiology is the basic reproduction number,
usually denoted by R0. This factor can measure the average
potential transmissibility of the disease. In a practical analysis,
the R0 how many expected cases could be generated by a single
primary case in a population where all invidious are susceptible.
Theoretically, this property does not vary in a stabilized contagions
situation due to the virus’s supposed and predetermined nature.
However, the virus’s biological characteristics are not constant, and
health policy measures change the number of susceptible people
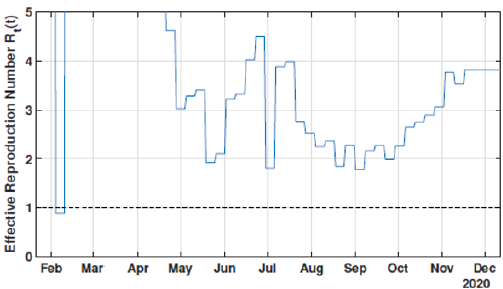
over time. The effective reproduction number Rt represents how the
pandemic, indeed, is spreading. In a dynamic systems viewpoint, Rt
calculates the epidemic velocity. If Rt > 1, the infection is spreading,
and the number of infected people increases at the beginning of the
epidemic. Otherwise, if Rt < 1 it means more individuals leaving from
the infected class than new infections occurring, either recovering
or dying and, therefore, the epidemic ceases.
,
wherein 0 N is the initial population size (before the contagion).
Moreover, the term β (t ) I (t ) / N (t ) represents the average number
of contacts that is sufficient for viral transmission from one
susceptible individual, per unit of time. Also, β (t ) I (t ) / N (t ) S (t )
counts as the total number of new cases from the number of
susceptible individuals, per unit of time. Another essential
information in epidemiology is the basic reproduction number,
usually denoted by R0. This factor can measure the average
potential transmissibility of the disease. In a practical analysis,
the R0 how many expected cases could be generated by a single
primary case in a population where all invidious are susceptible.
Theoretically, this property does not vary in a stabilized contagions
situation due to the virus’s supposed and predetermined nature.
However, the virus’s biological characteristics are not constant, and
health policy measures change the number of susceptible people
over time. The effective reproduction number Rt represents how the
pandemic, indeed, is spreading. In a dynamic systems viewpoint, Rt
calculates the epidemic velocity. If Rt > 1, the infection is spreading,
and the number of infected people increases at the beginning of the
epidemic. Otherwise, if Rt < 1 it means more individuals leaving from
the infected class than new infections occurring, either recovering
or dying and, therefore, the epidemic ceases.
As will be seen later, the effective reproduction number is given according to the epidemiological parameters calculated and the registered social distancing index along time.
Identification Algorithm
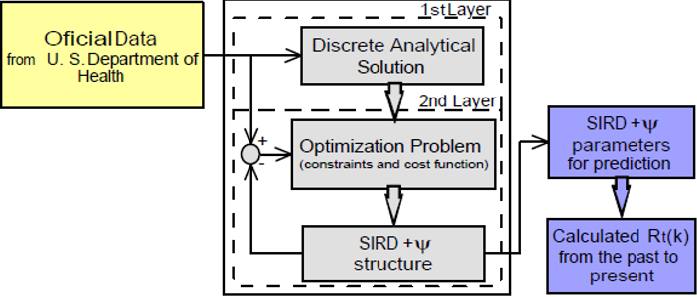
Recent numerical algorithms have been applied to calculate the parameters of the COVID-19 model [30-33]. Nonetheless, due to the degree of freedom given by Eq. 1, different parametric values can produce equivalent results in relation to the number of susceptible, infected, recovered, and deceased individuals. In other words, there is no one unique solution for the parameters which solver the numerical estimators. Although mathematical and graphical criteria have been used to validate these dynamic models when compared with real data, different values for the same parameters affect the epidemic characterization, for instance, the effective reproduction number (Rt). Therefore, in order to be able to describe the pandemic behavior, especially for forecast and control, it is proposed a two-step identification method for the parameters β (t ) , γ (t ) and ρ (t ) . As the first step, this procedure includes a discrete analytical formulation derived from Eq. 1 and, subsequently, an optimization algorithm based on the Ordinary Least Square minimization method to adjust the found parameters in a small defined bound. Thus, the algorithm developed here ensures appropriate parameters that characterize the epidemic’s reality since analytical calculations are used from the SIRD + Ψ model concepts, and it can adjust the model responses according to the official data.
As the published data are available with a sampling time of T1 and the proposed algorithm organizes time series packs of T2 units of time used as calculus basis, the first layer calculates the exact values of the parameters from a discrete analytical mode as follows:
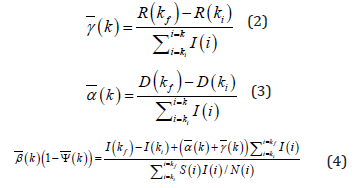
wherein k = 1,2,3...j with j = Tp/T2 being the number of time series packs and Tp the pandemic duration. Ψ(k ) is the average social mobility index within the interval of the time series pack k, delimited by the first and last points which are ki and kf, respectively. Furthermore, note that, for any generic parameter, χ (t ) = χ (k ) , in which ( ) 2, 2 t∈ k −1 T kT . Nevertheless, assuming that the data might be corrupted by minor issues, for instance, cases that are not reported in the day and are accumulated for the next day, or misreported cases, the calculated parameters are strictly adjusted by the second layer (optimization stage). This method allows improving identification reliability since this situation has been seen in different countries [26]. Once again, the available real data from the same interval i, f i∈k k are used to minimize the OLS problem, providing the data vector S, I, R and D. On the optimization loop, a dynamic SIRD + Ψ model takes into account the decision variables β , γ , α and the initial values S(ki), I(ki), R(ki) and D(ki) to estimate the values of I, R and D from ki to kf . At each interaction, the optimization layer minimizes the error between the real data and its estimated values from the SIRD + Ψ model choosing the decision variables accordingly, β , γ , α . The error is then calculated as:
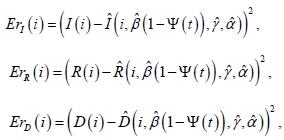
for which the variables Iˆ, Rˆ,Dˆ are estimated according to the SIRD +ψ model equations. The complete optimization problem is formulated as follows:
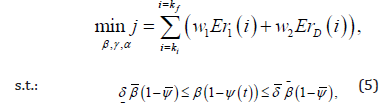
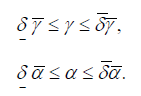
wherein δ and δ are the uncertainty interval to define the lower and upper bound of each decision variable on the optimization problem, and w1 w2 are taken as positive weighting values tuning parameters, used to normalize the magnitude order of the total cost concerning variables ErI and ErR.
The optimization algorithm employs a window of kf − k i + 1 units of time. The second layer finally provides as output the optimal values opt β , opt γ and opt α that can be used for forecasting and control and to calculate the effective reproduction number Rt. The algorithm also fit the SIRD +ψ model curve with real data using the optimal parameters. It is worth mentioning that this is an innovative and fundamental advantage of the method proposed in this work: to identify the relation between real social mobility, which may be used as a means of control strategy, and the parameters of the current pandemic. As depicted in the work of Fernandez-Villaverde and Jones [34], dealing the SIRD +ψ model with β associated with social distancing, the effects on the epidemic can be analyzed as a function of transmission rate inherent to the virus and health policies, which connects the model better and improves accuracy to fit data. As a result, the proposed methodology allows reliable forecasting, mainly regarding stringency formulations.
The parameters β , γ , ρ , and ψ are used to calculate the pandemic growth velocity since they are related to the rate of infected invidious. Thus, assuming that, at the beginning of the pandemic, S ≈ N Rt can be approximated as follows:
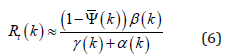
Design of Parameterization and Implementation
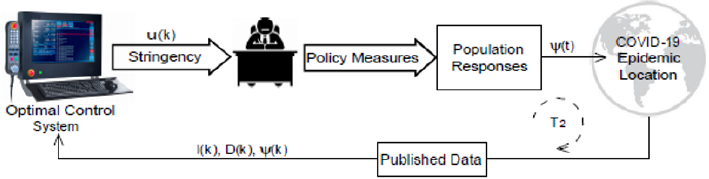
Since government data sources disclose daily samples of the pandemic dynamics, counting the infections cases and deaths, the unit of time as calculus basis used in the algorithm is day. Therefore, it is intuitive to choose a sampling time of T1 = 1 day for the discretetime dynamics samples in the interval i. Still, as the algorithm organizes the data in time series packs composed of each T2 days, T2 is tuned as the disease’s average incubation period. Thus, each estimated epidemiological parameter χ (k ) refers to the pandemic’s dynamics behavior for each T2 days along the time. Finally, the proposed identification algorithm is illustrated by the system shown in Figure 1. The procedure starts collecting the available real data from the first (k = 1) time series pack of T2 days split into T1 sample periods within the interval points ,i f i∈k k . Using the number of active infected I(i), recovered R(i), and fatal D(i) cases, the epidemiological parameters are calculated in the first layer of the system through the Eqs. 2, 3 and 4 . Considering the data are reliable, the obtained parameters define the epidemiological characteristics properly since the set of equations provides a unique solution. Nonetheless, noises and small errors mislead the measurements. Thus, these parameters are sent to the second layer, where a fine-tuning using the optimization algorithm ensures the best values to improve the dynamics curves. In this sense, in each period of T2 days, we have the epidemiological parameters to calculate the current pandemic situation using the Rt and simulate scenarios and predictions. These stages run continuously in the loop until the epidemic ends.
Results and Discussion
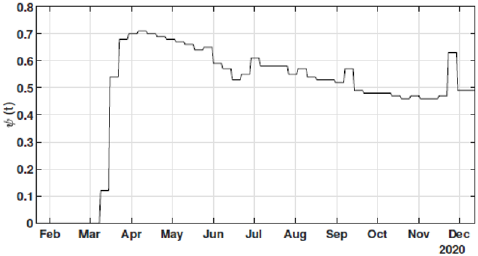
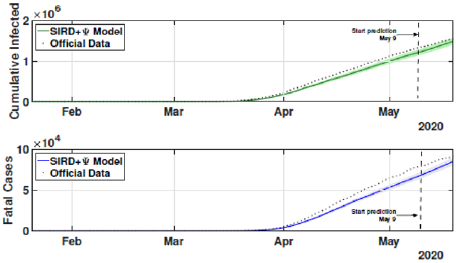
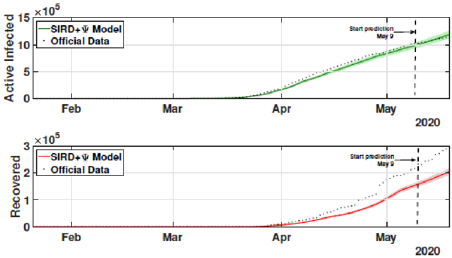
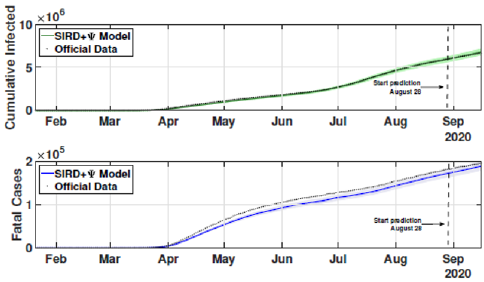
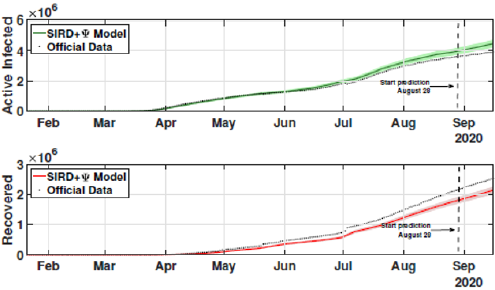
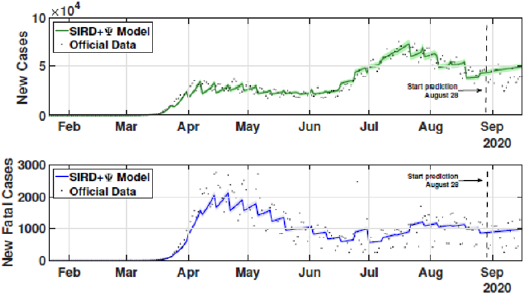
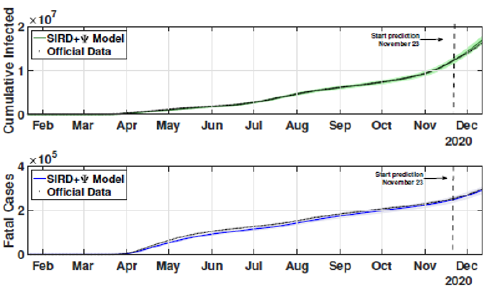
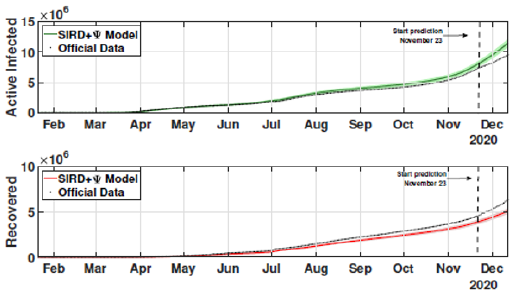
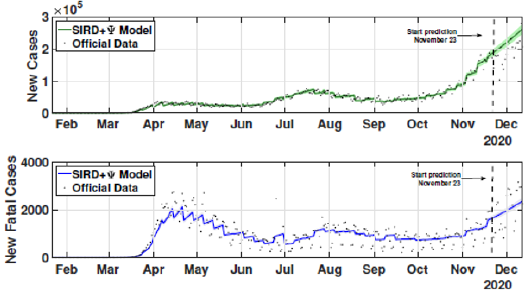
The identification procedure considers the number of cumulative cases, cumulative deaths, and active infected cases, for which we use the available dataset from official entities [35-37]. In this scenario, we propose the identification algorithm for T1 = 1 and T2 = 14 days, which means that the model is simulated every day and the parameters would slightly change every two weeks. For the social distancing index, we consider the rates provided by OpenPath [35]. This metric considers people’s access patterns and entries in workplaces and several locations, including business facilities, gyms, healthcare stations, government locations, and educational centers. The methodology is to compare people’s access to these locations to their accesses before the COVID-19 pandemic, thus, being possible to illustrate the social mobility trend around the country. Figure 2 illustrates the social distancing index in the United States from March 8, 2020, until December 12, 2020 for each week. In this section, we present the results of the identification procedure. In order to improve the model fit, we propose the weighing gains of the cost function in Eq. 5 as w1 = 1 and w2 = 25. Moreover, we define the uncertainty intervals as 10% to parameters γ and α , and 20% to parameter beta, since the inclusion of the variable Ψ(t ) can add noise in the model dynamic and compromise the identification robustness. We propose 3 scenarios to analyze the performance and reliability of the identification procedure, diving the data set in 3 periods: the first one is from February 1 to May 20, defined as the beginning of the pandemic using 120 days of data. The second scenario goes beyond, until September 17, where it is related to the middle period of the pandemic, using 240 days of data. The last scenario is the current stage of the pandemic, wherein the data goes until December 13, totaling 327 days of data. For the model curves, we proposed a error margin of 10% as an extrapolation of the identified model dynamics. The pandemic curves for validating the first scenario with identification algorithm are depicted in Figures 3-5. In this stage, it was used 110 days to identify the parameters considering the sample time of T2. The last 10 days are used as prediction of the model, in which the last identified values of β , γ and α are kept constants in this forecast period, as well as the last value of Ψ(t ) . It can be noticed that the curves of cumulative infected cases and deaths preset a very well fit. However, the new cases, new deaths recovered, and active infections curves still present an error between the real data and the curves. These results are expected since the algorithm considers the error minimization only for the cumulative cases and deaths, while the other curves are not considered in the identification procedure. Nevertheless, when it is inputted more information into the identification procedure, all curves’ fitting improves.
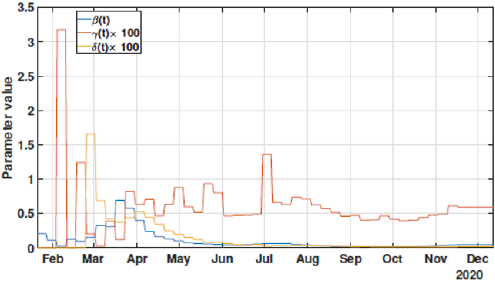
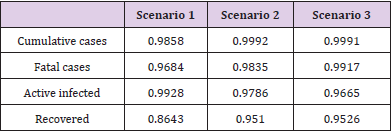
These effects can be shown in Figures 6-8. In these cases, we used the first 224 day to identify the model parameters to the same time window T2 = 14 days, and we use the last 16 days to validate the estimated pandemic curves. As can be seen, the model curves and the data agreement improves, including for the curves of new cases, new deaths, active infected individuals, and recovered cases. Moreover, since the model fit improves with more available data, it allows the designer to perform longer forecasting periods, significantly influencing control strategies’ design. Finally, we perform the identification procedure to the total available dataset, using the 327 days (also, with T2 = 14 days). In this last scenario, we still perform the validation stage using the last 20 days, keeping the last identified parameters constants in the forecast period. The parameters are identified to the first 307 days of data considering. Figure 9 shows the identified parameters for the last scenario and Figures 10-12 show the pandemic model curves and the real data. The effective reproduction number of all time including the three scenarios is shown in Figure 13. Although the Rt values found are consistent, it is important to highlight that its estimations depend on the measured data and, thereby, unreported or delayed reported cases produce some errors in these calculations. Furthermore, to illustrate the model fit, we propose the coefficient of determination metrics, R-square, which analyzes how properly the dataset can be explained by the model curves given by the percentage variation between both variables. The more the Rsquare approaches 1, the more reliable the identified model is to represent the dataset. Table 1 depicts the R-square coefficients for the three proposed scenarios.
Perspectives of Control Engineering Applications
As commented before, the field of control engineering may offer interesting solutions for the COVID-19 pandemic. In this area, mathematical theorems, computational algorithms, and engineering projects are developed to interfere in dynamic systems aiming at specific objectives. In particular, dynamic optimization techniques are particularly appropriate in pandemic situations because they can deal with nonlinear, unstable, multivariable, and complex systems [38]. We can cite the algorithms of Dynamic Real-time Optimization (D-RTO) and Model Predictive Control (MPC) that differentiate themselves very solely in few concepts and elements. In general, the conventional MPC is a type of D-RTO, since it applies an optimization problem for tracking. On the other hand, the D-RTO operates processes in an economic viewpoint [38,39]. The fact is that for any of these strategies, a valid model is crucial to assure reliable predictions and optimal conditions. Also, at least one manipulated variable is required to control other variables in any system. Thus, the proposed identification algorithm presented in this work ensures the applicability of control systems on the COVID19 pandemic, associating the social mobility index as manipulated variable, updating epidemiological parameters, and validating the model in real-time from collected data.
The approach is to propose optimal levels of social mobility considering economic and health aspects. As can be seen in Figure 14, the control system calculates optimal stringency values (u(k)) to guide public administration guidelines. Based on a pattern that describes health policies as a function of stringency values, governmental measures are elaborated, and public decrees are applied to the population. Thus, a new social mobility and responses from the human behavior are obtained, producing new social distancing dynamics (ψ (t )) and, hence, changing the epidemic velocity. Finally, for every T2 days, updated data feed the control system to determinate new stringency measures during the epidemic. The control system uses internally the proposed identification algorithm to calculate the optimal solutions. Also, with the historical data, the population responses must be modeled according to policy measures. A simple first-order equation with nonlinear gains is proposed by Morato et al. [30] and demonstrated by Pataro et al. [27] with relevant results. Therefore, the system presented here has a real possibility to be implemented in practice.
Conclusion
The paper proposed an identification algorithm able to calculate epidemiological parameters considering the social distance effects. The procedure uses a SIRD+ Ψ structure and discrete analytical solutions to ensure correct parameters according to measured data and the epidemiological concepts. The pandemic’s velocity can be estimated using the effective reproduction number, and simulations and forecasts are performed to support decisionmaking. The proposed scenarios have shown that the estimated model dynamics become more precise with more data. These results are achieved by performing the procedure for identifying parameters using a moving window associated with the real data. When it is provided more numerous and reliable data to the algorithm, the better is the model fitting results. Moreover, this can benefit algorithm forecasting, providing longer predictions with small errors. Furthermore, the parameter identification algorithm is adjustable and can be tuned in various manners to accomplish finely adjusted curves. The cost function can be customized to include other compartments to minimize the error or be chosen different weight constants to prioritize the optimized variable. According to the data fidelity used to estimate the model curves, the uncertainty bounds can also be changed. The sample time of the parameters change can be chosen to adjust the local data situation correctly. Finally, it is demonstrated that control engineering can be an alternative to deal with the pandemic if no enough vaccines are still available. The proposed algorithm can be incorporated into a control system to offer an adaptive model and predictions that allow optimal social distancing guidance. Thus, future works including dynamic optimization and applications will be done to investigate the impact in the U.S.
References
- Lu R, Zhao X, Li J, Niu P, Yang B, et al. (2020) Genomic characterisation and epidemiology of 2019 novel coronavirus: implications for virus origins and receptor binding, The Lancet 395(10224): 565-574.
- Breban R, Riou J, Fontanet A (2013) Interhuman transmissibility of middle east respiratory syndrome coronavirus: estimation of pandemic risk. The Lancet 382(9893): 694 -699.
- Adhikari SP, Meng S, Wu YJ, Mao YP, Ye RX, et al. (2020) Epidemiology, causes, clinical manifestation and diagnosis, prevention and control of coronavirus disease (covid-19) during the early outbreak period: a scoping review, Infectious Diseases of Poverty 9(1): 29.
- Kırbas I, Sozen A, Tuncer AD, Kazancıoglu FS (2020) Comparative analysis and forecasting of covid-19 cases in various european countries with ARIMA, NARNN and LSTM approaches, Chaos, Solitons & Fractals 138: 1-7.
- Sarkar K, Khajanchi S, Nieto JJ (2020) Modeling and forecasting the covid-19 pandemic in india, Chaos, Solitons & Fractals 139: 1-16.
- Willis MJ, V HG Díaz VH G, Prado-Rubio OA, Stosch MV (2020) Insights into the dynamics and control of covid-19 infection rates, Chaos, Solitons & Fractals 138: 1-7.
- Brauer F, Castillo-Chavez C, Feng Z (2019) Mathematical Models in Epidemiology, Springer-Verlag New York, London, England.
- Kermack WA (1927) McKendrick, Contributions to the mathematical theory of epidemics-i, Proceedings of the Royal Society 115A: 700-721.
- Wu JT, Leung K, Bushman M, Kishore N, Niehus R, et al. (2020) Estimating clinical severity of covid-19 from the transmission dynamics in wuhan, china, Nature Medicine 26(4): 506-510.
- Postnikov EB (2020) Estimation of covid-19 dynamics “on a back-of-envelope”: Does the simplest sir model provide quantitative parameters and predictions?, Chaos, Solitons & Fractals 135: 1-6.
- Malavika B, Marimuthu S, Joy M, Nadaraj A, Asirvatham ES, et al. (2020) Forecasting covid-19 epidemic in india and high incidence states using sir and logistic growth models, Clinical Epidemiology and Global Health.
- Annas S, Pratama MI, Rifandi M, W Sanusi W, Side S (2020) Stability analysis and numerical simulation of seir model for pandemic covid-19 spread in indonesia (pre-proof). Chaos, Solitons & Fractals.
- Rajagopal K, Hasanzadeh N, Parastesh F, Hamarash II, Jafari S, et al. (2020) A fractional-order model for the novel coronavirus (covid-19) outbreak. Nonlinear Dynamics.
- Lee C, Li Y, Kim J (2020) The susceptible-unidentified infected-confirmed (suc) epidemic model for estimating unidentified infected population for covid-19. Chaos, Solitons & Fractals 139: 110090.
- Higazy M (2020) Novel fractional order sidarthe mathematical model of covid-19 pandemic. Chaos, Solitons & Fractals 138: 1-19.
- Anirudh A (2020) Mathematical modeling and the transmission dynamics in predicting the covid-19 - what next in combating the pandemic, Infectious Disease Modelling 5: 366-374.
- Smith BA (2020) A novel idea: The impact of serial interval on a modified-incidence decay and exponential adjustment (m-idea) model for projections of daily covid-19 cases. Infectious Disease Modelling 5: 346-356.
- Khan FM, Gupta R (2020) Arima and nar based prediction model for time series analysis of covid-19 cases in india, Journal of Safety Science and Resilience 1: 12-18.
- Aslam M (2020) Using the kalman filter with arima for the covid-19 pandemic dataset of Pakistan. Data in Brief 31: 1-6.
- Americano Da Costa MV, Narasimhan A, Guillen D, Joseph B, Goswami DY (2020) Generalized distributed state space model of a CSP plant for simulation and control applications: Single-phase flow validation, Renewable Energy Journal 153: 36-48.
- Americano da Costa MV, Pasamontes M, Normey-Rico JE, Guzman JL, Berenguel M (2014) Advanced control strategy combined with solar´ cooling for improving ethanol production in fermentation units. Ind Eng Chem Res 53: 11384-11392.
- De Araujo RG B, Americano Da Costa MV, Joseph B, Guzman JL (2020) Developing professional and entrepreneurship skills of engineering´ students through problem-based learning: A case study in brazil. International Journal of Engineering Education 36: 155-169.
- Pataro IM, Americano da Costa MV, Joseph B (2020) Closed-loop dynamic real-time optimization (CL-DRTO) of a bioethanol distillation process using an advanced multilayer control architecture, Computers & Chemical Engineering 143: 1-14.
- Kohler J, Schwenkel L, Koch A, Berberich J, Pauli P, et al. (2020) Robust and optimal predictive control of the covid-19 outbreak. Annual Reviews in Control.
- Morato MM, Pataro I, Americano da Costa MV, Normey-Rico JE (2020) Optimal control concerns regarding the covid-19 (sars-cov-2) pandemic in bahia and santa catarina, brazil. in: Brazilian Automation Conference.
- Morato MM, Pataro IM, Americano da Costa MV, Normey-Rico JE (2020) A parametrized nonlinear predictive control strategy for relaxing COVID-19 social distancing measures in brazil. ISA Transactions.
- Pataro IM L, Oliveira JF, Morato MM, Amad AA S, Ramos PI P, et al. (2021) A control framework to optimize public health policies in the course of the covid-19 pandemic, medRxiv.
- Peng L, Yang W, Zhang D, Zhuge C, Hong L (2020) Epidemic analysis of COVID-19 in China by dynamical modeling.
- Kucharski AJ, Russell TW, Diamond C, Liu Y, Edmunds J, et al. (2020) Early dynamics of transmission and control of COVID-19: a mathematical modelling study, The lancet infectious diseases 20(5): 553-558.
- Morato MM, Bastos SB, Cajueiro DO, Normey-Rico JE (2020) An optimal predictive control strategy for covid-19 (sars-cov-2) social distancing policies in brazil, Annual Reviews in Control 50: 417-431.
- Sarkar K, Khajanchi S, Nieto JJ (2020) Modeling and forecasting the covid-19 pandemic in india. Chaos, Solitons & Fractals 139: 1-16.
- Sun T, Wang Y (2020) Modeling covid-19 epidemic in heilongjiang province, china. Chaos, Solitons & Fractals 138: 1-5.
- Kennedy DM, Zambrano GJ, Wang Y, Neto OP (2020) Modeling the effects of intervention strategies on covid-19 transmission dynamics, Journal of Clinical Virology 128: 1-7.
- Fernandez-Villaverde J, Jones CI (2020) Estimating and Simulating a SIRD Model of COVID-19 for Many Countries, States, and Cities. NBER Working Papers 27128, National Bureau of Economic Research, Inc.
- (2021) OpenPath, Social distancing index.
- (2021) T new York Times, Coronavirus (covid-19) data in the united states.
- Dong E, Du H, Gardner L (2020) An interactive web-based dashboard to track covid-19 in real time. 20(5): 533-534.
- Brosilow C, Joseph B (2020) Techniques of Model-based Control, Prentice-Hall, New Jersey.
- Pataro I, Americano da Costa MV, Roca L, Sanches JLG, Berenguel M (2020) An economic D-RTO for thermal solar plant: analysis and simulations based on a feedback linearization control case, in Brazilian Automation Conference.

 Research Article
Research Article