ABSTRACT

The dependence of the integral heat transfer distribution on the Prandtl number for turbulent convective heat exchange in a pipe with a sequence of periodic protrusions of semicircular geometry is investigated by a computational method based on the numerical solution of the system of Reynolds equations closed using the Menter shear stress transfer model and the energy equation on multi-scale intersecting structured grids. The calculation was carried out on the basis of a theoretical method based on the solution of the Reynolds equations by a factorized finite-volume method, closed using the Menter shear stress transfer model, and the energy equation on multi-scale intersecting structured grids (FCOM). The calculations carried out in the work showed that with an increase in the Prandtl number at small Reynolds numbers, first there is a noticeable increase in the relative heat exchange, and then the relative heat exchange changes less, and for small steps there is an increase in it, for medium - almost stabilization, for large - a slight decrease. At large Reynolds numbers, the relative heat transfer decreases with an increase in the Prandtl number with its further stabilization. The study analyzed the calculated dependences of the relative heat transfer on the Prandtl number Rg at different values of the relative height of the turbulator h/D, the relative step between the turbulators t/D, at different values of the Reynolds number Re, all other things being equal, which showed qualitative and quantitative changes in the calculated parameters. The analytical justification of the calculated regularities obtained is that for small Reynolds numbers, the height of the turbulator is less, and for large ones-less than the height of the wall layer, therefore, only the flow core is turbulized, which only leads to an increase in hydraulic resistance and to an exaggeration of heat transfer. In the work, on the basis of limited computational material, a noticeable decrease in the level of heat transfer intensification for small Prandtl numbers was theoretically confirmed. The obtained results of intensified heat transfer in the region of low Prandtl numbers justify the promising development of research in this direction. The theoretical data obtained in this work determined the regularities of relative heat transfer in a wide range of Prandtl numbers, including in those areas where experimental material does not yet exist.

Keywords: Modeling; Numerical; Channel; Pipe; Convective; Menter Model; Turbulator; Heat Transfer; Hydraulic Resistance; Prandtl Number

Overview

The application of periodic protrusions on the walls of the washed surfaces is a well-tested method of vortex intensification of heat exchange [1-3]. The intensification of heat transfer for the conditions of the flow of heat carriers in pipes with turbulators has been carried out and is being carried out mainly by experimental methods [1-3], and theoretical studies are quite few, many of them are based on integral approaches [4-8]. At the present stage of research, the problems of aeromechanics and thermophysics of separation and vortex flows are increasingly being solved by the methods of multi-block computing technologies based on intersecting structured grids [9-13]. The present study is a logical continuation of the above computational methods [14-25] for the analysis of turbulent flow and heat exchange in pipes with semicircular flow turbulators (diaphragms) with different relative heights, steps for different modes of coolant flow in order to analyze in more detail the intensification of heat exchange for heat carriers with different Prandtl numbers. Previously, this aspect was not fully investigated.

Mathematical and Discrete Models

In this paper, a system of Reynolds and energy equations written in natural variables is solved using completely implicit finite-difference schemes on a centered non-uniform skew-angle grid. To calculate the pressure field, the SIMPLEC procedure is used; the principle of splitting by physical processes takes place. The convective terms are approximated using a quadratic counterflow scheme. The difference equations are solved using a highly efficient method of incomplete matrix factorization with accelerated convergence using the additive correction method. A multi-block algorithm for solving the problem on intersecting multi-scale grids, tested in solving problems of vortex dynamics and heat transfer [9], is used for the correct description of turbulent heat transfer. The description of turbulent transport is implemented using the zonal low-Reynolds Menter model [13]. The study considered channels of constant cylindrical cross-section with eight turbulators located on the walls in the form of periodic diaphragms of semicircular cross-section. The parameters were changed in the following ranges: d/D=0.95¸0.92; t/D=0.25¸1, where it is the placement step of the turbulators; d is the diameter of the diaphragm; D is the pipe dimeter; Re=104¸105 is the Reynolds number; Pr=1¸20 is the Prandtl number (for limited calculations -Pr=1¸0.05). Briefly, the calculation model can be characterized as follows.

The three-dimensional computational domain under study has several sections, each of which consists of a single protrusion (Figure 1). The calculation assumes that with the considered number of turbulators, the turbulent flow becomes steady. In the main part of the study, the calculation of heat transfer was carried out under a boundary condition on a wall of the first kind with a sequential change in the Prandtl number from 1 to 20 in order to establish the regularity of changes in the intensification of heat transfer for various heat carriers. At the preliminary stage of the study, a modification of a multidisciplinary computational complex for numerical modeling of spatial separation flows and vortex heat exchange is carried out in order to adapt and refine the mathematical model of flow and vortex heat exchange in channels with turbulators, assuming the emergence of spatial vortex structures responsible for the vortex intensification of heat exchange processes in the wall zones of pipes with turbulators.

Figure 1:The pipe grid consisting of several sections with a semicircular turbulator located in the middle, the input and output smooth sections.

In order to solve the problem of intensified heat transfer, the calculated three-dimensional grid was constructed in the same way: a two-dimensional grid was constructed in axial and radial coordinates, unfolded along the circumferential coordinate with a constant step. In order to achieve the necessary resolution in the vicinity of the obstacle, two-dimensional grids were used in the form of multi-tiered structured grids, and the obstacle was described on the most detailed grid with the highest spatial resolution. The detailed grid was embedded in a coarser grid, which was used to describe the flow in the near track of the obstacle, and the transition from the wall area to the axis was also carried out using intermediate grids, the purpose of which was to increase the longitudinal step of the grid in the area of the obstacle and change the resolution along the circumferential coordinate. In the future, we will not dwell on the details of the model aspects of numerical calculations using this method, since they were considered in [2,5,9-11,13,15,16,18,19,23, 26].

Data for Initial Calculations

In the inlet section of the pipe section under consideration, a uniform flow with a thin boundary layer allowing for variation was considered; the turbulence parameters correspond to experimental tests in the pipe, assuming the turbulence scale of the order of the pipe diameter, which is chosen as the characteristic size, and the degree of turbulence is assumed to be one and a half percent. In the output section of the pipe section under consideration, “soft” boundary conditions are set, otherwise called solution continuation conditions, which are characterized by extrapolation of parameters outside the calculation area. On the walls of the pipe washed by the coolant, which are considered isothermal under boundary conditions of the first kind and have a temperature greater or lower by a certain number of degrees with respect to the temperature of the incoming flow, there are adhesion conditions. For the selected channel geometry, each individual problem from several sections is solved in two stages: first, the dynamic problem is solved, after which the thermal problem for various Prandtl numbers is solved for the pre-calculated fields of the flow velocity components and turbulence characteristics. The convergence criteria for the dynamic problem are determined by limiting the errors in calculating the Cartesian components of the velocity, and for the thermal problem - by limiting the increment of heat fluxes on the walls; in this work, the value 0.0001 was taken as a relative error.

Influence of the Prandtl Number on Heat Transfer in Straight Round Pipes with Periodically Arranged Surface Turbulators of a Semicircular Cross- Section Flow at Various Geometric and Operating Parameters

The resistance coefficient ξ and the averaged Nusselt number Nu for a pipe with semicircular turbulators during turbulent convective heat exchange in this paper were determined by the calculation method based on the numerical solution of the system of Reynolds equations closed using the Menter shear stress transfer model and the energy equation on multi-scale intersecting structured grids. The adequacy of the applied method is justified by the fact that earlier for comparison in [5,15-17,19- 20,22-24] similar experimental data on heat transfer and hydraulic resistance were used for pipes with semicircular turbulators or diaphragms, where there was a good correlation between theory and experiment. Identified in the author’s previous theoretical works (for example, in [5,15-17,19-20,22-24]) the adequacy of the existing experimental data of the implemented computational model for local and averaged characteristics of flow and heat exchange in pipes with turbulators determines its application in order to identify the regularity of integral (averaged) parameters of heat exchange in pipes with different Prandtl numbers, depending on the geometry of the channel and the flow regime of the coolant.

In this study, only the most common turbulators of semicircular cross-section, characteristic of pipes with diaphragms, are considered. This question is important, since it is necessary to know for which Prandtl numbers there is a higher intensification of heat transfer depending on the determining parameters. The calculation of the intensified heat exchange according to this factorized control-volumetric method was carried out for the most characteristic geometric and regime characteristics for pipes with turbulators (d/D=0.92; 0.90; t/D=0.25; 0.50; 1.00; Re=104; 105) [1-3] for a fairly wide range of Prandtl numbers, Pr=1÷20. As an illustration of the calculated data obtained by this method, Fig. 2-4 shows the characteristic calculated current lines for pipes with transverse annular turbulators of semicircular cross-section for the considered flow conditions for closed (Figure 2), semi-open (Figure 3) and open (Figure 4) depressions (classification according to [5- 8]), respectively. The values of the relative heat transfer Nu/NuGL for various Prandtl numbers, all other things being equal, were calculated for isothermal flow at equivalent parameters for both pipes with and without turbulators.

Figure 2:Calculated current lines for a closed cavity in a pipe with turbulators with a semicircular cross-section at Re=105; d/ D=0.92; t/D=0.25.

Figure 3: Calculated current lines for a semi-open cavity in a pipe with turbulators with a semicircular cross-section at Re=104; d/D=0.95; t/D=0.25.

Figure 4:Calculated current lines for an open cavity in a pipe with turbulators with a semicircular cross-section at Re=104; d/ D=0.92; t/D=1.00.

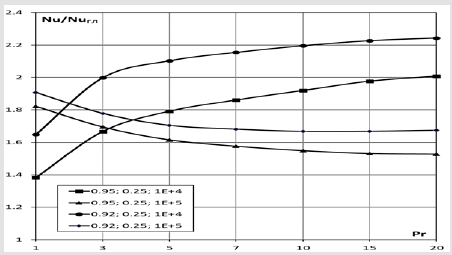
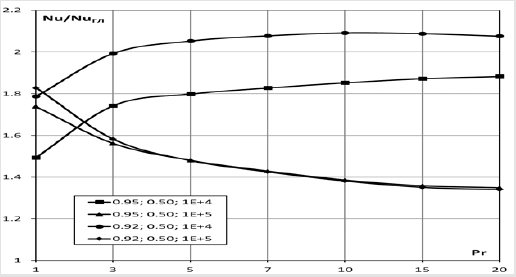
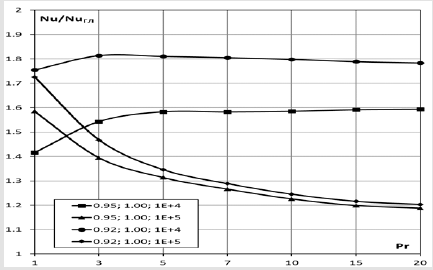
The obtained calculation results based on the proposed model for the above range of determining parameters are shown in (Figure 5-7), where they are distributed over small (t/ D=0.25), medium (t/D=0.50) and large (t/D=1.00) steps between turbulators. As can be seen from (Figure 5-7), for relatively small Reynolds numbers (Re=104), first there is a noticeable increase in the relative heat exchange of Nu/Nu with an increase in the Prandtl number, then the relative heat exchange changes less: for small steps, there is an increase in it, for medium - almost stabilization, for large - a slight decrease. For relatively large Reynolds numbers (Re=105), there is a decrease in the relative heat transfer with an increase in the Prandtl number, with its practical stabilization for the largest values from the considered range of Prandtl numbers. The difference in the patterns of changes in relative heat transfer depending on the Prandtl number (Figure 5-7) is justified by the fact that for small Reynolds numbers, the height of the turbulator is less than the height of the wall layer [1-3,26-27], and for large Reynolds numbers-less.

Figure 5:Calculated values of the relative heat transfer Nu/NuGL for t/D=0.25; d/D=0.92 and 0.90; Re=104 and 105 depending on the Prandtl number Rg=1÷20.

Figure 6:Calculated values of the relative heat transfer Nu/NuGL for t/D=0.50; d/D=0.92 and 0.90; Re=104 and 105 depending on the Prandtl number Rg=1÷20.

Figure 7:Calculated values of the relative heat transfer Nu/NuGL for t/D=1.00; d/D=0.92 and 0.90; Re=104 and 105 depending on the Prandtl number Rg=1÷20.

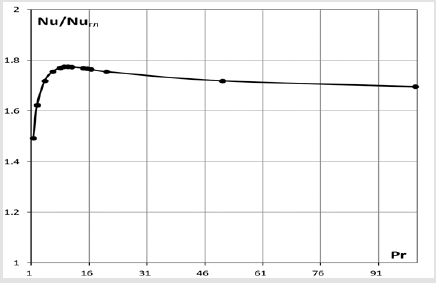
Figure 8:Calculated values of the relative heat transfer Nu/NuGL for d/D=0.912; t/D=0.50; Re=104 depending on the Prandtl number Rg=1÷100.

Figure 9:Calculated current lines for the flow in a pipe with turbulators of semicircular cross-section at Re=104; d/D=0.912; t/D=0.50.

The latter causes turbulence only of the flow core, increasing only the hydraulic resistance, almost without increasing the heat exchange. Experimental confirmation of the given theoretical data was given in the works [1-3,26-27], where the actual experiments of the authors, the experiments [28], as well as the regularities for the limiting heat transfer are analyzed [1-3,26-27]. Another confirmation of the calculated numerical dependences obtained is the data of analytical solutions for intensified heat transfer obtained using a modified four-layer model of a turbulent boundary layer [4-5,7-8]. Within the framework of this work, calculations were performed for conditions similar to those characteristic of the above-mentioned experiments [13] (d/D=0.912; t/D=0.50; Re=104; Pr=1,15÷6,7) [1-2, 3], which are shown in Fig. 8 (the calculated current lines are shown in Fig. 9), from which it can be seen that the theoretical nature of the change in relative heat transfer from the Prandtl number is completely similar to the experiment [1-2, 3]. In classical works on intensified heat exchange [1-2, 3], it is indicated that there are no reliable experimental data, but it is assumed that artificial turbulization of liquid metal flows should have low efficiency [1-2, 3].

Within the framework of this work, the simulation of intensified heat exchange during the flow of liquid metals in only a limited range was carried out, since this aspect is not the main one for this work, which showed that the relative heat exchange for the conditions of the above experiments [28] decreases by 12% for Rg=0.5 relative to the relative heat exchange for Rg=1; similar decreases for Rg=0.1 and Rg=0.05 are 37% and 40%, respectively. Therefore, it is theoretically confirmed that the intensified heat exchange for liquid metals is lower than for gaseous heat carriers. The above is also confirmed by the data of analytical solutions for intensified heat transfer obtained using a modified four-layer model of a turbulent boundary layer [4- 5, 7-8]. The theoretical calculated data obtained in the work for a limited range of determining parameters on a decrease in the level of heat exchange intensification for small Prandtl numbers determine the prospects of this scientific direction - in the future, using this model, it will be possible to calculate the relative heat exchange in pipes with diaphragms for liquid metals for a wide range of channel geometry and the flow regime of the coolant. The above analysis indicates that the theoretical data fully correspond to the existing experimental material, significantly overlapping the range of the determining parameters of the latter. The theoretical data made it possible to identify patterns of relative heat transfer depending on the Prandtl number in those areas where there are no reliable experimental data yet.

Conclusion

1. The calculation method developed and used in this study, based on the solution of the Reynolds equations by the finite-volume method, closed using the Menter shear stress transfer model and the energy equation on multi-scale intersecting structured grids, allowed us to calculate the relative heat transfer in pipes with semicircular annular turbulators for heat carriers with different Prandtl numbers with acceptable accuracy.

2. The study analyzed the calculated dependences of the relative heat transfer on the Prandtl number Rg at different values of the relative height of the turbulator h/D, the relative step between the turbulators t/D, at different values of the Reynolds number Re, all other things being equal, which showed qualitative and quantitative changes in the calculated parameters.

3. The calculations carried out in the work showed that with an increase in the Prandtl number for small Reynolds numbers, first there is a noticeable increase in the relative heat exchange, and then the relative heat exchange changes less, and for small steps there is an increase in it, for medium - almost stabilization, for large - a slight decrease.

4. For large Reynolds numbers, the relative heat transfer decreases with an increase in the Prandtl number with its further stabilization.

5. The analytical justification of the calculated regularities obtained is that for small Reynolds numbers, the height of the turbulator is less, and for large ones - less than the height of the wall layer, therefore, only the flow core is turbulized, which only leads to an increase in hydraulic resistance and to an exaggeration of heat transfer.

6. In the work, on the basis of limited computational material, a noticeable decrease in the level of heat transfer intensification for small Prandtl numbers was theoretically confirmed. The obtained results of intensified heat transfer in the region of low Prandtl numbers justify the promising development of research in this direction.

The theoretical data obtained in the work determined the regularities of relative heat transfer in a wide range of Prandtl numbers, including in those areas where experimental material does not yet exist.

References

1. Kalinin E K, Dreitser G A, jarcho S A (1972) Intensification of heat transfer in the channels. M: Mashinostroenie, p. 220.
2. Kalinin E K, Dreitzer G A, Yarkho S A (1990) Intensification of heat transfer in channels. Moscow: Mashinostroenie, p. 208.
3. EK Kalinin, GA Dreitser, IZ Kopp (1998) Effective heat transfer surface M Energoatomizdat, p. 408
4. Dreitzer G A, Lobanov I E (2003) Modeling of isothermal heat exchange under turbulent flow in channels under conditions of heat exchange intensification. Heat and power engineering 1: 54-60.
5. Lobanov I E (2005) Mathematical modeling of intensified heat transfer during turbulent flow in channels: Dissertation for the degree of Doctor of Technical Sciences M, pp. 632.
6. Lobanov I E (2002) Modeling of heat exchange and resistance under turbulent flow in the channels of heat carriers with variable physical properties under the conditions of heat exchange intensification. Proceedings of the Third Russian National Conference on Heat Exchange. In 8 volumes. Vol. 6. Intensification of heat exchange. Radiation and complex heat transfer M: Publishing House of the MEI, pp. 144-147.
7. Lobanov I E, Paramonov N V (2011) Mathematical modeling of intensified heat transfer during flow in channels based on complex models of a turbulent boundary layer. Moscow MAI Publishing House, p. 160.
8. Lobanov I E, Stein L M (2010) Promising heat exchangers with an intensified heat exchange for metallurgical production. (General theory of intensified heat transfer for heat exchangers used in modern metallurgical production.) In 4 volumes. Volume III. Mathematical modeling of intensified heat transfer during turbulent flow in channels using multilayer, super-multilayer and compound models of a turbulent boundary layer. M MGAKHiS, p. 288.
9. A V Ermishin, S A Isaev, M. St. Petersburg (2001) Control of the flow of bodies with vortex cells in an application to integrated layout aircraft (numerical and physical modeling), p. 360.
10. S A Isaev, A I Leontiev, A E Usachov (1998) Numerical study of the jet-vortex mechanism of heat and mass transfer intensification in the vicinity of a spherical well on a plane when an incompressible viscous liquid flow around it, taking into account the influence of shape asymmetry, natural convection and non-stationary processes. Proceedings of the Second Russian National Conference on Heat Exchange. In 8 volumes. Vol. 6. Intensification of heat exchange. Radiation and complex heat transfer M: MEI Publishing House, p. 121-124.
11. A D Gosmen, VM Pan, AK Ranchel (1986) Numerical methods for studying viscous fluid flows M. Mir, p. 234.
12. Yu A Bystrov, S A Isaev, N A Kudryavtsev, A I Leontiev (2005) Numerical modeling of vortex intensification of heat transfer in pipe packs. SPb: Sudostroenie, p. 398.
13. Menter F R (1994) Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J 32(8): 1598.
14. S A Isaev, I E Lobanov, OA Boyarkina (2010) Vortex intensification of convective heat exchange during turbulent flow of air and oil in pipes and channels with periodic elements of discrete roughness Proceedings of the Fifth Russian National Conference on Heat Exchange. In 8 volumes. Volume 6. Intensification of heat exchange. Radiation and complex heat exchange. M: MEI, pp. 84-87.
15. Dreitzer G A, Isaev S A, Lobanov I E (2005) Calculation of convective heat transfer in a pipe with periodically located surface flow turbulators. Thermophysics of high temperatures 43(2): 223-230.
16. Dreitser G A, Isaev S A, Lobanov I E (2004) Calculation of convective heat transfer in a pipe with periodic protrusions. Vestnik MAI T 11(2): 28-35.
17. Dreitzer G A, Isaev S A, Lobanov I E (2003) Calculation of convective heat transfer in a pipe with periodic protrusions. Problems of gas dynamics and heat and mass transfer in power plants: Proceedings of the XIV School-seminar of young scientists and specialists under the guidance of Academician of the Russian Academy of Sciences A. I. Leontiev. Moscow: MEI, T 1: 57-60.
18. S A Isaev, P A Baranov, I E Lobanov (2011) Intensification of heat transfer in tubes with a volume and a surface vortex generator for inhomogeneous fluids heat and mass transfer and hydrodynamics in swirling flows: the Fourth international conference: abstracts. M Publishing house MPEI S, p. 66.
19. Kalinin E K, Lobanov I E (2008) Problems of studying heat exchange processes in single-phase media flows at the stage of successful development of numerical modeling. Abstracts of reports and reports of the VI Minsk International Forum on Heat and Mass Transfer. Minsk 1: 101-103.
20. Lobanov I E, Kalinin E K (2011) Theoretical study, comparison with experiment of current lines and kinetic energy components of turbulent pulsations in vortex structures in pipes with turbulators. Branch aspects of technical sciences 12: 4-15.
21. Lobanov I E (2013) Mathematical modeling of the dynamics of the development of vortex structures in pipes with turbulators. Moscow Scientific Review. 12: 9-15.
22. Lobanov I E (2012) Modeling of the structure of vortex zones between periodic surface-located turbulators of a rectangular cross-section flow. Mathematical modeling 24(7): 45-58.
23. Lobanov I E (2012) Structure of vortex zones between periodic surface-located turbulators of a rectangular cross-section flow. Electronic scientific journal Research of Technical Sciences 2(4): 18-24.
24. Lobanov I E (2013) Theoretical study of the kinetic energy of turbulent pulsations and its components in pipes with turbulators. Moscow Scientific Review 1: 23-30.
25. Lobanov I E, Antyukhov I V (2013) Modern problems of heat exchange intensification in channels with the help of periodically surface-located turbulators of a rectangular cross-section flow. Fundamental and applied problems of engineering and technology 3-2(299): 22-27.
26. Migay V K (1987) Modeling of heat-exchange power equipment. L: Energoatomizdat Leningrad Branch, p. 263.
27. Migay V K (1980) Improving the efficiency of modern heat exchangers. L: Energiya. Leningrad Branch, pp. 144.
28. Hustrup R C, Sabersky R H, Bartz D F, Noel M B (1958) Jet Propulsion. 28(4): 259-263.

Abstract

The dependence of the integral heat transfer distribution on the Prandtl number for turbulent convective heat exchange in a pipe with a sequence of periodic protrusions of semicircular geometry is investigated by a computational method based on the numerical solution of the system of Reynolds equations closed using the Menter shear stress transfer model and the energy equation on multi-scale intersecting structured grids. The calculation was carried out on the basis of a theoretical method based on the solution of the Reynolds equations by a factorized finite-volume method, closed using the Menter shear stress transfer model, and the energy equation on multi-scale intersecting structured grids (FCOM). The calculations carried out in the work showed that with an increase in the Prandtl number at small Reynolds numbers, first there is a noticeable increase in the relative heat exchange, and then the relative heat exchange changes less, and for small steps there is an increase in it, for medium - almost stabilization, for large - a slight decrease. At large Reynolds numbers, the relative heat transfer decreases with an increase in the Prandtl number with its further stabilization. The study analyzed the calculated dependences of the relative heat transfer on the Prandtl number Rg at different values of the relative height of the turbulator h/D, the relative step between the turbulators t/D, at different values of the Reynolds number Re, all other things being equal, which showed qualitative and quantitative changes in the calculated parameters. The analytical justification of the calculated regularities obtained is that for small Reynolds numbers, the height of the turbulator is less, and for large ones-less than the height of the wall layer, therefore, only the flow core is turbulized, which only leads to an increase in hydraulic resistance and to an exaggeration of heat transfer. In the work, on the basis of limited computational material, a noticeable decrease in the level of heat transfer intensification for small Prandtl numbers was theoretically confirmed. The obtained results of intensified heat transfer in the region of low Prandtl numbers justify the promising development of research in this direction. The theoretical data obtained in this work determined the regularities of relative heat transfer in a wide range of Prandtl numbers, including in those areas where experimental material does not yet exist.

Keywords: Modeling; Numerical; Channel; Pipe; Convective; Menter Model; Turbulator; Heat Transfer; Hydraulic Resistance; Prandtl Number